Gesture Recognition by Using Depth Data: Comparison of Different Methodologies
In the last decade, gesture recognition has been attracting a lot of attention as a natural way to interact with computer and/or robots through intentional movements of hands, arms, face, or body. A number of approaches have been proposed giving particular emphasis on hand gestures and facial expressions by the analysis of images acquired by conventional RGB cameras.
The recent introduction of low cost depth sensors, such as the Kinect camera, allowed the spreading of new gesture recognition approaches and the possibility of developing personalized human computer interfaces. The Kinect camera provides RGB images together with depth information, so the 3D structure of the scene is immediately available. This allows us to easily manage many tasks such as people segmentation and tracking, body part recognition, motion estimation, and so on. Recently human activity recognition and motion analysis from 3D data have been reviewed in a number of interesting works.
At present, Gesture Recognition through visual and depth information is one of the main active research topics in the computer vision community. The launch on the market of the popular Kinect, by the Microsoft Company, influenced video‐based recognition tasks such as object detection and classification and in particular allowed the increment of the research interest in gesture/activity recognition. The Kinect provides synchronized depth and color (RGB) images where each pixel corresponds to an estimate of the distance between the sensor and the closest object in the scene together with the RGB values at each pixel location. Together with the sensor some software libraries are also available that permit to detect and track one or more people in the scene and to extract the corresponding human skeleton in real time. The availability of information about joint coordinates and orientation has promoted a great impulse to research on gesture and activity recognition.
Many papers, presented in literature in the last years, use normalized coordinates of proper subset of skeleton joints which are able to characterize the movements of the body parts involved in the gestures. Angular information between joint vectors has been used as features to eliminate the need of normalization in Ref.
Different methods have been used to generate gesture models. Hidden Markov Models (HMM) are a common choice for gesture recognition as they are able to model sequential data over time. Usually HMMs require sequences of discrete symbols, so different quantization schemes are first used to quantize the features which characterize the gestures. Support vector machines (SVM) reduce the classification problem into multiple binary classifications either by applying a one‐versus‐all (OVA‐SVM) strategy (with a total of N classifiers for N classes) or a one‐versus‐one (OVO‐SVM) strategy (with a total of N×(N−1)/2N×(N−1)/2 classifiers for N classes). Artificial neural networks (ANNs) represent another alternative methodology to solve classification problems in the context of gesture recognition. The choice of the network topology, the number of nodes/layers and the node activation functions depends on the problem complexity and can be fixed by using iterative processes which run until the optimal parameters are found.
Distance‐based approaches are also used in gesture recognition problems. They use distance metrics for measuring the similarity between samples and gesture models. In order to apply any metric for making comparisons, these methods have to manage the problem related to the different length of feature sequences. Several solutions have been proposed in literature: Dynamic Time Warping technique (DTW) is the most commonly used. It calculates an optimal match between two sequences that are nonlinearly aligned. A frame‐filling algorithm is proposed in Ref. to first align gesture data, then an eigenspace‐based method (called Eigen3Dgesture) is applied for recognizing human gestures.
In the last years, the growing interest in automatically learning the specific representation needed for recognition or classification has fostered the recent emergence of deep learning architectures. Rather than using handcrafted features as in conventional machine learning techniques, deep neural architectures are applied to learn representations of data at multiple levels of abstractions in order to reduce the dimensionality of feature vectors and to extract relevant features at higher level. Recently, several approaches have been proposed such as in Refs. In Ref., a method for gesture detection and localization based on multiscale and multimodel deep learning is presented. Both temporal and spatial scales are managed by employing a multimodel convolutional neural network. Similarly in Ref., a multimodel gesture segmentation and recognition method, called deep dynamic neural networks, is presented. A semisupervised hierarchical dynamic framework based on a Hidden Markov Model is proposed for simultaneous gesture segmentation and recognition.
In this chapter, we compare different methodologies to approach the problem of Gesture Recognition in order to develop a natural human‐robot interface with good generalization ability. Ten gestures performed by one user in front of a Kinect camera are used to train several classifiers based on different approaches such as dynamic time warping (DTW), neural network (NN), support vector machine (SVM), hidden Markov model (HMM), and deep neural network (DNN).
The performance of each methodology is evaluated considering several tests carried out on depth video streams of gestures performed by different users (diverse from the one used for the training phase). This performance analysis is required as users perform gestures in a personalized way and with different velocity. Even the same user executes gestures differently in separate video acquisition sessions. Furthermore, contrarily to the case of static gesture recognition, in the case of depth videos captured live the problem of gesture segmentation must be addressed. During the test phase, we apply a sliding window approach to extract sequences of frames to be processed and recognized as gestures. Notice that the training set contains gestures which are accompanied by the relative ground truth labels and are well defined by their start and end points. Testing live video streams, instead, involves several challenging problems such as the identification of the starting/ending frames of a gesture, the different length related to the different types of gestures and finally the different speeds of execution. The analysis of the performance of the different methodologies allows us to select, among the set of available gestures, the ones which are better recognized together with the better classifier, in order to construct a robust human‐robot interface.
In this chapter, we consider all the mentioned challenging problems. In particular, the fundamental steps that characterize an automatic gesture recognition system will be analyzed: (1) feature extraction that involves the definition of the features that better and distinctively characterize a specific movement or posture; (2) gesture recognition that is seen as a classification problem in which examples of gestures are used into supervised and semisupervised learning schemes to model the gestures; (3) spatiotemporal segmentation that is necessary for determining, in a video sequence, where the dynamic gestures are located, i.e., when they start and end.
The rest of the chapter is organized as follows. The overall description of the problem and the definition of the gestures are given in Section 2. The definition of the features is provided in Section 3. The methodologies selected for the gesture model generation are described in Section 4. Section 6 presents the experiments carried out both in the learning and prediction stage. Furthermore, details on gesture segmentation will be given in the same section. Finally, Section 7 presents the final conclusions and delineates some future works.
Problem definition
In this chapter, we consider the problems related to the development of a gesture recognition interface giving a panoramic view and comparing the most commonly used methodologies of machine learning theory. At this aim, the Kinect camera is used to record video sequences of different users while they perform predefined gestures in front of it. The OpenNI Library is used to detect and segment the user in the scene in order to obtain the information of the joints of the user’s body. Ten different gestures have been defined. They are pictured in Figure 1. Throughout the chapter the gestures will be referred by using the following symbols G1, G2, G3, … GN, where N=10. Some gestures are quite similar in terms of variations of joint orientations; the only difference is the plane in which the bones of the arm rotate. This is the case, for example, of gestures G9 and G4 or G1, and G8. Furthermore, some gestures involve movements in a plane parallel to the camera (G1, G3, G4, G7) while others involve a forward motion in a plane perpendicular to the camera (G2, G5, G6, G8, G9, G10). In the last case, instability in detecting some joints can occur due to auto occlusions.
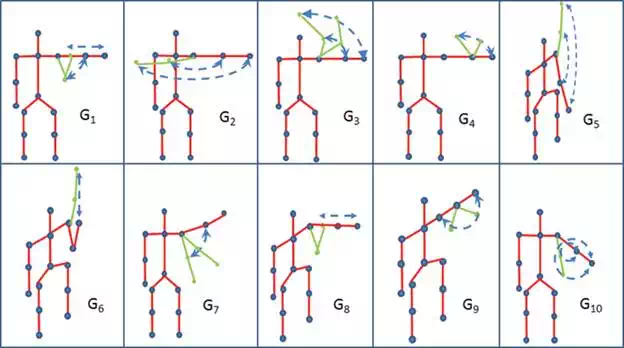
FIGURE 1.
Ten different gestures are shown. Gestures G1G1, G3G3, G4G4, and G7G7 involve movements in a plane parallel to the camera. Gestures G2G2, G5G5, G6G6, G8G8, G9G9, and G10G10 involve a forward motion in a plane perpendicular to the camera.
The proposed approaches for gesture recognition involve three main stages: a feature selection stage, a learning stage and a prediction stage. Firstly the human skeleton information, captured and returned by the depth camera, is converted into representative and discriminant features. These features are used during the learning stage to learn the gesture model. In this chapter, different methodologies are applied and compared in order to construct the gesture model. Some methodologies are based on a supervised or semisupervised process such as neural network (NN), support vector machine (SVM), hidden Markov model (HMM), and deep neural network (DNN). Dynamic time warping (DTW) is a distance‐based approach, instead. Finally, during the prediction stage new video sequences of gestures are tested by using the learned models. The following sections will describe in detail each stage previously introduced.
Feature selection
The complexity of the gestures strictly affects the feature selection and the choice of the methodology for the construction of the gesture model. If gestures are distinct enough, the recognition can be easy and reliable. So, the coordinates of joints, which are immediately available by the Kinect software platforms, could be sufficient. In this case a preliminary normalization is required in order to guarantee invariance with respect to the height of the users, distance and orientation with respect to the camera. On the other hand, the angular information of joint vectors has the great advantage of maximizing the invariance of the skeletal representation with respect to the camera position. In Ref., the angles between the vectors generated by the elbow‐wrist joints, and the shoulder‐elbow joints, are used to generate the models of the gestures. The experimental results, however, prove that these features are not discriminant enough to distinguish all the gestures.
In our approach, we use more complex features that represent orientations and rotations of a rigid body in three dimensions. The quaternions of two joints (shoulder and elbow) of the left arm are used. A quaternion comprises a scalar component and a vector component in complex space and is generally represented in the following form:
![]()
where the coefficients a,b,c,d are real numbers and i,j,k are the fundamental quaternion units. The quaternions are extremely efficient to represent three‐dimensional rotations as they combine the rotation angles together with the rotation axes. In this work, the quaternions of the shoulder and elbow joints are used to define a feature vector Vi for each frame ii:
![]()
where the index ss stands for shoulder and ee stands for elbow. The sequence of vectors of a whole gesture execution is defined by the following vector:
![]()
Where nn is the number of frames during which the gesture is entirely performed.
Learning stage: gesture model construction
The learning stage regards the construction of the gesture model. As introduced in Section 1, machine learning algorithms are largely and successfully applied to gesture recognition. In this context, gesture recognition is considered as a classification problem. So, under this perspective, a number of gesture templates are collected, opportunely labeled with the class labels (supervised learning) and used to train a learning scheme in order to learn a classification model. The constructed model is afterwards used to predict the class label of unknown templates of gestures.
In this chapter, different learning methodologies are applied to learn the gesture model. For each of them, the best parameter configuration and the best architecture topology which assure the convergence of each methodology are selected. Artificial neural networks (ANNs), support vector machines (SVMs), hidden Markov models (HMMs), and deep neural networks (DNNs) are the machine learning algorithms compared in this chapter. Furthermore a distance‐based method, the dynamic time warping (DTW), is also applied and compared with the aforementioned algorithms. The following subsections will give a brief introduction of each algorithm and some details on how they are applied to solve the proposed gesture recognition problem.
NEURAL NETWORK
A neural network is a computational system that simulates the way biological neural systems process information. It consists of a large number of highly interconnected processing units (neurons) typically distributed on multiple layers. The learning process involves successive adjustments of connection weights, through an iterative training procedure, until no further improvement occurs or until the error drops below some predefined reasonable threshold. Training is accomplished by presenting couples of input/output examples to the network (supervised learning).
In this work, 10 different neural networks have been used to learn the models of the defined gestures. The architecture of each N consists of an input layer, one hidden layer and an output layer with a single neuron. The back‐propagation algorithm is applied during the learning process. Each training set contains the templates of one gesture as positive examples and those of all the others as negative ones. As each gesture execution lasts a different number of frames, a preliminary normalization of the feature vectors has been carried out by using a linear interpolation. Linear interpolation to resample the number of features is a good compromise between computational burden and quality of results. The length of a feature vector V, which describes one single gesture, has been fixed to n=60. This length has been fixed considering the average time of execution of each type of gesture which is about 2 seconds and the sample rate of the Kinect camera which is 30 Hz.
SUPPORT VECTOR MACHINE
Support vector machine is a supervised learning algorithm widely used in classification problems. The peculiarity of SVM is that of finding the optimal separating hyperplane between the negative and positive examples of the training set. The optimal hyperplane is defined as the maximum margin hyperplane, i.e., the one for which the distance between the hyperplane (decision surface) and the closest data points is maximum. It can be shown that the optimal hyperplane is fully specified by a subset of data called support vectors which lie nearest to it, exactly on the margin.
In this work, SVMs have been applied considering the one‐versus‐one strategy. This strategy builds a two‐class classifier for each pair of gesture classes. In our case, the total number of SVMs is defined by:
![]()
where NN is the number of gesture classes. The training set of each SVM contains the examples of the two gesture classes for which the current classifier is built. As in the case of NNs, the feature vectors are preliminary normalized to the same length nn.
HIDDEN MARKOV MODEL
Hidden Markov model is a statistical model which assumes that the system to be modeled is a Markov process. Even if the theory of HMMs dates back to the late 1960s, their widespread application occurred only within the past several years. Their successful application to speech recognition problems motivated their diffusion in gesture recognition as well. An HMM consists of a set of unobserved (hidden) states, a state transition probability matrix defining the transition probabilities among states and an observation or emission probability matrix which defines the output model. The goal is to learn the best set of state transition and emission probabilities, given a set of observations. These probabilities completely define the model.
In this work, one discrete hidden Markov model is learnt for each gesture class. The feature vectors of each training set, which represent the observations, are firstly normalized and then discretized by applying a K‐means algorithm. A fully connected HMM topology and the Baum‐Welch algorithm have been applied to learn the optimal transition and emission probabilities.
DEEP NEURAL NETWORK
Deep learning is a relatively new branch of machine learning research. Its objective is to learn features automatically at multiple levels of abstraction exploiting an unsupervised learning algorithm at each layer. At each level a new data representation is learnt and used as input to the successive level. Once a good representation of data has been found, a supervised stage is performed to train the top level. A final supervised fine‐tuning stage of the entire architecture completes the training phase and improves the results. The number of levels defines the deepness of the architecture.
In this work, a deep neural network with 10 output nodes (one for each class of gesture) is constructed. It comprises two levels of unsupervised autoencoders and a supervised top level. The autoencoders are used to learn a lower dimensional representation of the feature vectors at a higher level of abstraction. An autoencoder is a neural network which is trained to reconstruct its own input. It is comprised of an encoder, that maps the input to the new representation of data, and a decoder that reconstruct the original input. We use two autoencoders with one hidden layer. The number of hidden neurons represents the dimension of the new data representation. The feature vectors of training set are firstly normalized, as described in Section 4.1, and fed into the first autoencoder. So the features generated by the first autoencoder are used as input to the second one. The size of the hidden layer for both the first and second autoencoder has been fixed to half the size of the input vector. The features learnt by the last autoencoder are given as input to the supervised top level implemented by using a softmax function trained with a scaled conjugate gradient algorithm [37]. Finally the different levels are stacked to form the deep network and its parameters are fine‐tuned by performing backpropagation using the training data in a supervised fashion.
DYNAMIC TIME WARPING
DTW is a different technique with respect to the previously described ones as it is a distance‐based algorithm. Its peculiarity is to find the ideal alignment (warping) of two time‐dependent sequences considering their synchronization. For each pair of elements of the sequences, a cost matrix, also referred as local distance matrix, is computed by using a distance measure. Then the goal is to find the minimal cost path through this matrix. This optimal path defines the ideal alignment of the two sequences. DTW is successfully applied to compare sequences that are altered by noise or by speed variations. Originally, the main application field of DTW was automatic speech processing, where variation in speed appears concretely. Successively DTW found its application in movement recognition, where variation in speed is of major importance, too.
In this work, DTW is applied to compare the feature vectors in order to measure how different they are for solving the classification problem. Differently from the previously described methodologies, the preliminary normalization of feature vectors is not required due to the warping peculiarity of DTW algorithm. For each class of gesture, one target feature vector is selected. This is accomplished by applying DTW to the set of training samples inside each gesture class. The one with the minimum distance from all the other samples of the same class is chosen as target gesture. Each target gesture will be used in the successive prediction stage for classification.
Prediction stage: gesture model testing
In prediction stage, also referred as testing stage, video sequences with unknown gestures are classified by using the learnt gesture models. This stage allows us to compare the recognition performance of the methodologies introduced in the learning stage. These methodologies have been applied by using different strategies as described in the following.
In the case of N, 10 classifiers have been trained, one for each class. So the feature vector of a new gesture sample is inputted into all the classifiers and is assigned to the class with the maximum output value.
In the case of SVM, instead, a max‐win voting strategy has been applied. The trained SVMs are 45 two‐class classifiers. When each classifier receives as input a gesture sample, classifies it into one of the two classes. Therefore, the winning class gets one vote. When all the 45 votes have been assigned, the instance of the gesture is classified into the class with the maximum number of votes.
In the case of HMM, 10 HMMs have been learnt during the learning stage, one for each class of gesture. As introduced in Section 4.3 the model of each class is specified by the transition and emission probabilities learnt in the learning stage. When a gesture instance is given as input to the HMM, this computes the probability of that instance given the model. The class of the HMM returning the maximum probability is the winning class.
In the case of DNN, as described in Section 4.4, the deep architecture, constructed in the learning stage, has 10 output nodes. So, when a gesture sample is inputted in the network for prediction, the winning class is simply the one relative to the node with the maximum output value.
Finally, for what concerns the DTW case, the target gestures, found during the learning stage, are used to predict the class of new gesture instances. The distances between the unknown gesture sample and the 1010 target gestures are computed. The winning class is that of the target gesture with minimum distance.
Experiments
In this section the experiments carried out in order to evaluate the performance of the analyzed methodologies will be described and the obtained results will be shown and compared. In particular, the experiments conducted in both the learning stage and the prediction stage will be detailed separately for a greater clarity of presentation.
Several video sequences of gestures performed by different users have been acquired by using a Kinect camera. Sequences of the same users in different sessions (e.g., in different days) have been also acquired in order to have a wide variety of data. The length of each sequence is about 1000 frames. The users have been requested to execute gestures standing in front of the Kinect, by using the left arm and without pause between one gesture execution and the successive one. The distance between Kinect and user is not fixed. The only constraint is that the whole user’s body has to be seen by the sensor, so its skeleton data can be detected by using the OpenNi processing Library. These data are recorded for each frame of the sequence.
LEARNING STAGE
As described in Section 4, the objective of the learning stage is to construct or, more specifically, to learn a gesture model. In order to reach this goal, the first step is the construction of the training datasets. The idea of using public datasets has been discarded as they do not assure that real situations are managed. Furthermore, they contain sample gestures which are acquired mainly in the same conditions. We have decided to use a set of gestures chosen by us (see Figure 1), which have been selected from the “Arm‐and‐Hand Signals for Ground Forces”.
The video sequences of only one user (afterward referred as Training User) are considered for building the training sets. Each sequence contains several executions of the same gesture without idle frames between one instance and the other. In this stage, we manually segment the training streams into gesture instances in order to guarantee that each extracted subsequence contains exactly one gesture execution. Then each instance is converted in feature vector by using the skeleton data as described in Section 3. Notice that feature vectors V can have different lengths, because either gesture execution lasts a different number of frames or users execute gestures with different speeds. Part of the obtained feature vectors are used for training and the rest for validation.
The second step of the learning stage is the construction of the gesture model by using the methodologies described in Section 4. A preliminary normalization of feature vectors to the same length is needed in the cases of NN, SVM, HMM, and DNN. As described in Section 4.1, nn has been fixed to 6060. So each normalized feature vector V has 480480 components which have been defined by using the quaternion coefficients of shoulder and elbow joints (see Eqs. (2) and(3)). In the case of DTW this normalization is not required.
For each methodology, different models can be learnt depending on the parameters of the methodology. These parameters can be structural such as the number of hidden nodes in the N architecture or in the autoencoder or the number of hidden states in a HMM; or they can be tuning parameters as in the case of SVM. So, different experiments have been carried out for selecting the optimal parameters inside each methodology. Optimal parameters have to be intended as those which provide a good compromise between over‐fitting and prediction error over the validation set.
PREDICTION STAGE
The prediction stage represents the recognition phase which allows us to compare the performance of each methodology. In this phase the class labels of feature vectors are predicted based on the learnt gesture model. Differently from the training phase that can be defined as an off‐line phase, the prediction stage can be defined as an on‐line stage. In this case the video sequences of six different users (excluded the Training‐User) have been properly processed by using an approach that works when live video sequences have to be tested. Differently from the learning stage, where gesture instances were manually selected from the sequences and were directly available for training the classifiers, in the prediction stage the sequences need to be opportunely processed by applying a gesture segmentation approach. This process involves several challenging problems such as the identification of the staring/ending points of a gesture instance, the different length related to the different classes of gestures and finally the different speeds of execution.
In this work, the sequences are processed by using a sliding window approach, where a window slides forward over the sequence by one frame per time in order to extract subsequences. First, the dimension of the sliding window must be defined. As there are no idle frames among successive gesture executions, an algorithm based on Fast Fourier Transform (FFT) has been applied in order to estimate the duration of each gesture execution. As each sequence contains several repetitions of the same gesture, it is possible to approximate the sequence of features as a periodic signal. Applying the FFT and by tacking the position of the fundamental harmonic component, the period can be evaluated as the reciprocal value of the peak position. The estimated period is then used to define the sliding window’s dimension in order to extract subsequences of features from the original sequence. Each subsequence represents the feature vector which is then normalized (if required) and provided as input to the classifier which returns a prediction label for the current vector. In order to construct a more robust human computer interface, a further verification check has been introduced before the final decision is taken. This process has been implemented by using a max‐voting scheme on 10 consecutive answers of the classifier obtained testing 10 consecutive subsequences. The final decision is that relative to the class label with the maximum number of votes.
RESULTS AND DISCUSSION
In Figures 2–7, the recognition rates obtained by testing the classifiers on a number of sequences performed by six different users are reported. For each user the plotted rates have been obtained by averaging the results over three testing sequences. As can be observed the classifiers behave in a very different way due to the personalized execution of gestures by the users. Furthermore, there are cases where some classifiers fail in assigning the correct class. This is, for example, the case of gestures G2and G4 performed by User 6 (see Figure 7). DTW has 0% detection rate for G2, whereas NN has 0%0%detection rate for G4. The same happens for gesture G9 performed by User 2 (see Figure 3) which is rarely recognized by all the classifiers, as well as G3 performed by User 5 (see Figure 6).
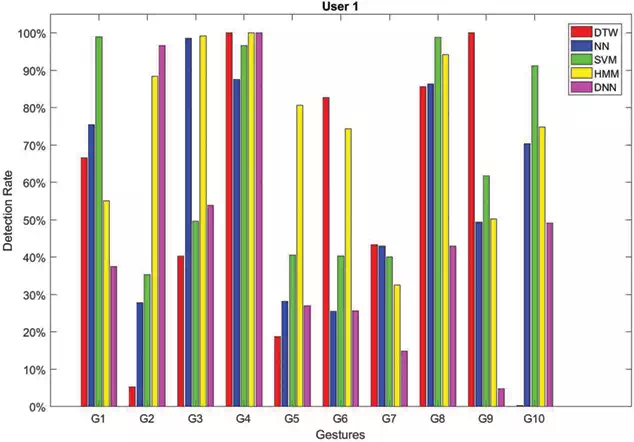
FIGURE 2.
Recognition rates obtained by testing each method on sequences of gestures performed by User 1.
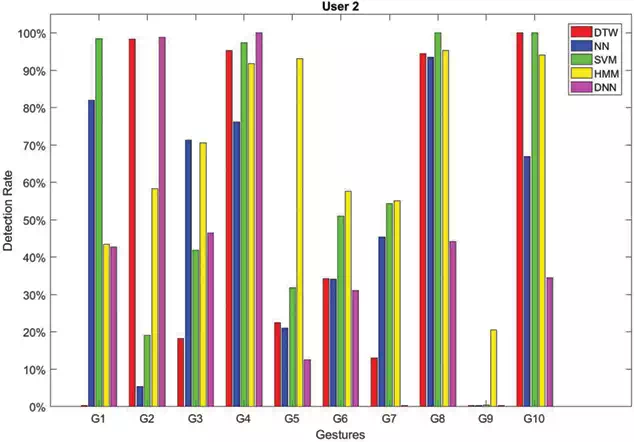
FIGURE 3.
Recognition rates obtained by testing each method on sequences of gestures performed by User 2.
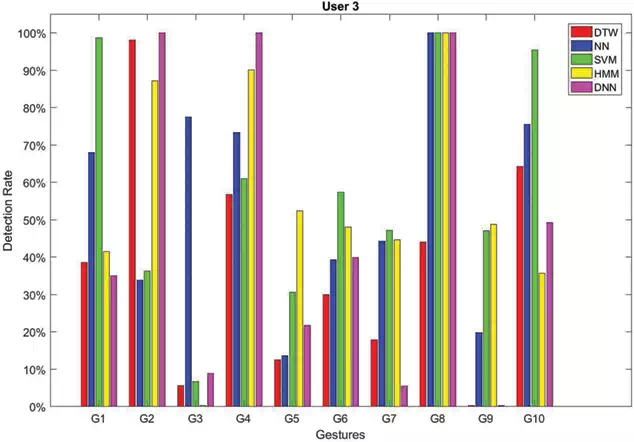
FIGURE 4.
Recognition rates obtained by testing each method on sequences of gestures performed by User 3.
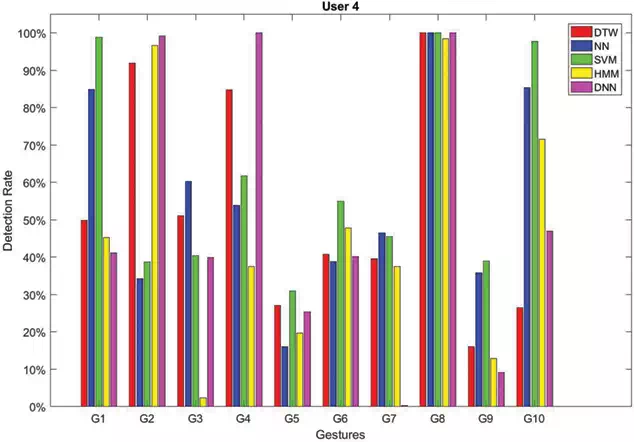
FIGURE 5.
Recognition rates obtained by testing each method on sequences of gestures performed by User 4.
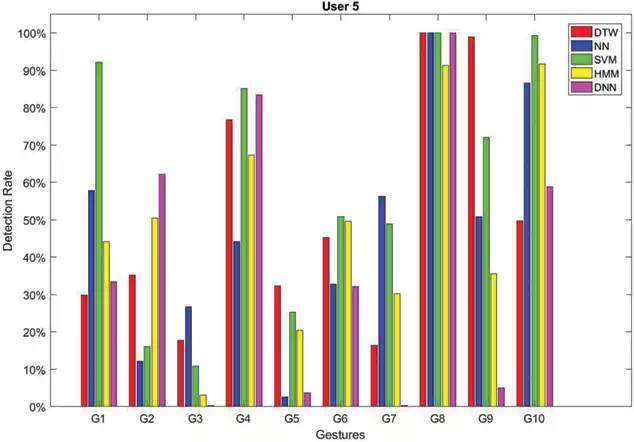
FIGURE 6.
Recognition rates obtained by testing each method on sequences of gestures performed by User 5.
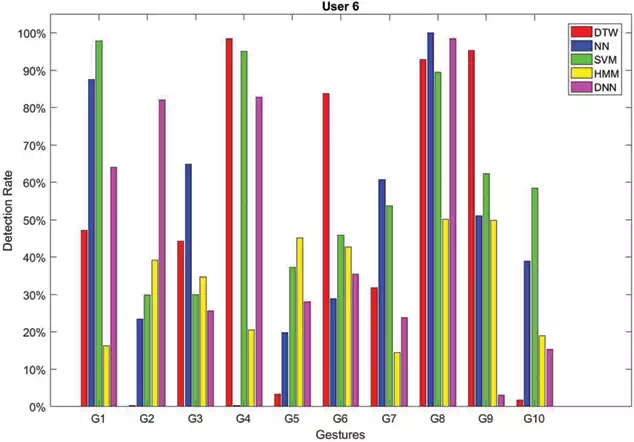
FIGURE 7.
Recognition rates obtained by testing each method on sequences of gestures performed by User 6.
In order to analyze the performance of classifiers when the same user is used in the learning and prediction phases, an additional experiment has been carried out. So the Training User has been asked to perform again the gestures. Figure 8 shows the obtained recognition rates. These results confirm the variability of classifiers performance even if the same user is used for training and testing the classifiers.
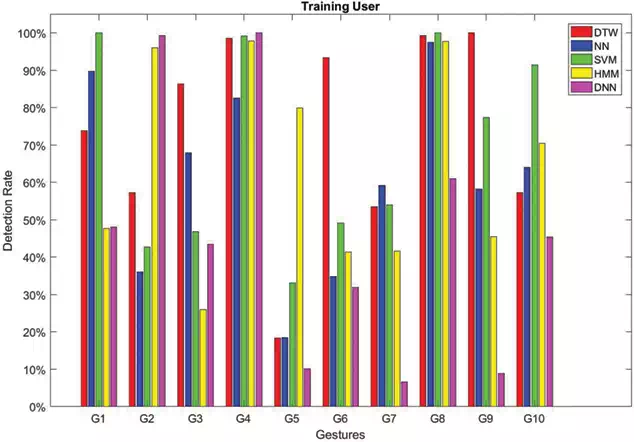
FIGURE 8.
Recognition rates obtained by testing each method on sequences of gestures performed by the Training User in a session different from the one used for the learning phase.
The obtained results confirm that it is difficult to determine the superiority of one classifier over the others because of the large number of variables involved that do not guarantee a uniqueness of gesture execution. These are for example: the different relative positions between users and camera, the different orientations of the arm, the different amplitude of the movement, and so on. All these factors can greatly modify the resulting skeletons and joint positions producing large variations in the extracted features.
Some important conclusions can be drawn from the experiments that have been carried out: the solution of using only one user to train the classifiers can be pursued as the recognition rates are quite good even if the gestures are performed in personalized way.
Another point concerns the complexity of the gestures used in our experiments. The results show that the failures are principally due either to the strict similarity between different gestures or to the fact that the gestures which involve a movement perpendicular with respect to the camera (not in the lateral plane) can produce false skeleton postures and consequently features affected by errors.
Moreover, some gestures have parts of the movement in common. Figures 9 and 10 have been pictured to better explain these problems.
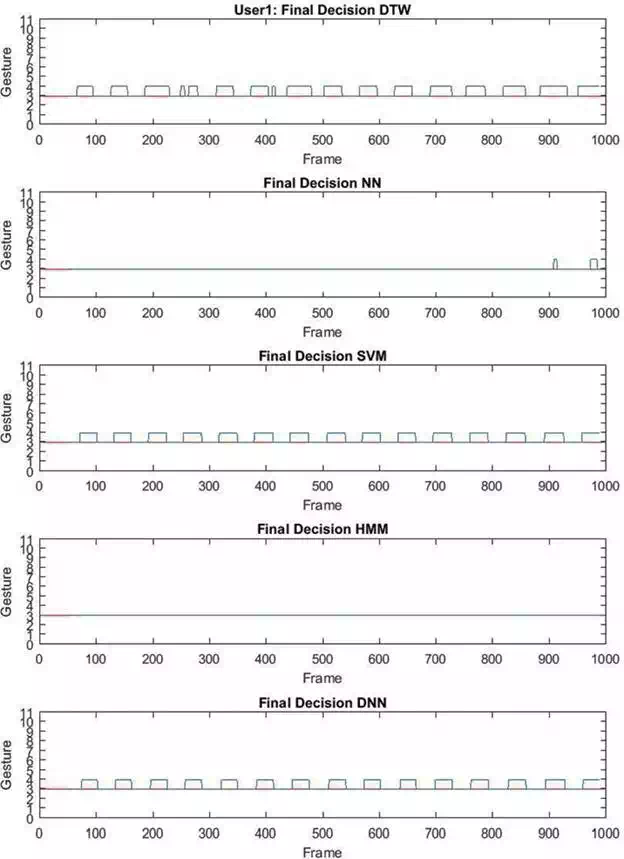
FIGURE 9.
Recognition results relative to the first 1000 frames of a test sequence relative to gesture G3G3performed by User 1. The x‐axis represents the frame number of the sequence and the y‐axis represents the gesture classes ranging from 1 to 10 (the range 0–11 has been used only for displaying purposes). The red line denotes the ground truth label (G3G3 in this case), whereas the blue one represents the predicted labels obtained from the classifiers.
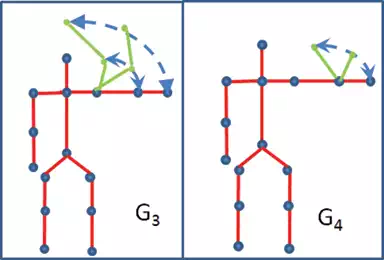
FIGURE 10.
Gesture G3 and G4. Both gestures involve a rotation of the arm in a plane parallel to the camera.
Figure 9 shows the results obtained by testing the first 1000 frames of a sequence of gesture G3 executed by User 1. Each plot in the figure represents the output of each classifier DTW, NN, SVM, HMM, and DNN, respectively. As can be seen in the case of DTW, SVM, and DNN, gesture G3 is frequently misclassified as gesture G4. Both gestures are executed in a plane parallel to the camera: G3 involves the rotation of the whole arm, whereas G4 involves the rotation of the forearm only (as can be seen in Figure 11). Notice that the misclassification happens principally in the starting part of gesture G3, which is very similar to the starting part of G4; therefore, they can be easily mistaken.
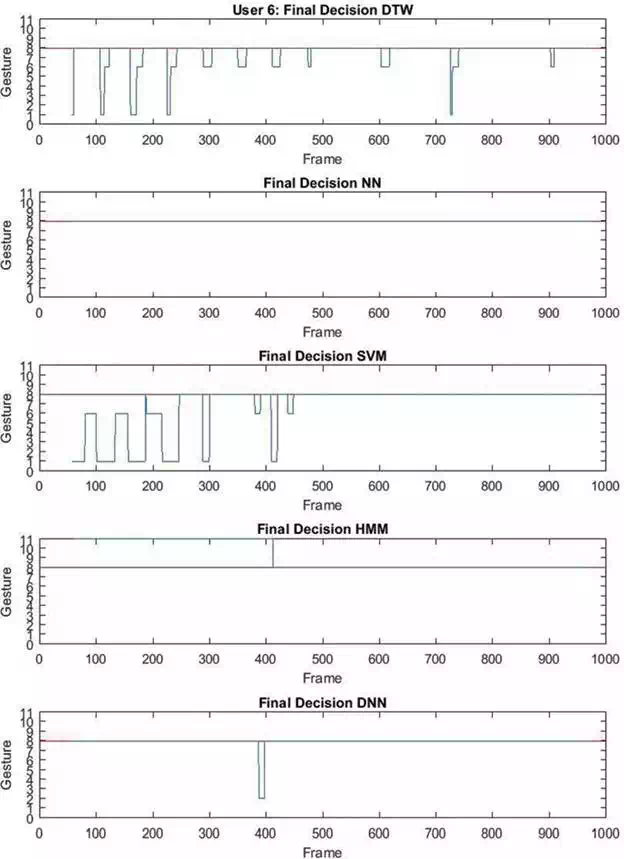
FIGURE 11.
Recognition results relative to the first 1000 frames of a test sequence relative to gesture performed by User 6. The x-axis represents the frame number of the sequence and the y-axis represents the gesture classes ranging from 1 to 10 (the range 0 -11 has been used only for displaying purposes). The red line denotes the ground truth label ( in this case), whereas the blue one represents the predicted labels obtained from the classifiers.
Furthermore in Figure 9, it is worth to notice the good generalization ability of NN and HMM. As can be seen in these cases, both classifiers are always able to recognize the gesture even when the sliding windows cover the frames between two successive gesture executions.
An additional observation can be taken considering G1 and G8 as an example. In Figure 12, notice that gesture G1 and gesture G8 involve the same rotations of the forearm, but performed in different planes with respect to the camera (the lateral one in the case of G1 and the frontal one in the case of G8). It is evident that a slight different orientation of the user in front of the camera while performing gesture G1 (risp. G8), could generate skeletons quite similar to those obtained by performing gesture G8 (risp. G1). Figure 10 shows the results relative to this case. As can be seen gesture G8G8 is sometimes misclassified as gesture G1 by DTW and SVM. A few misclassifications of gesture G8 as G6 are also present since G8 and G6 have some parts of movement in common.
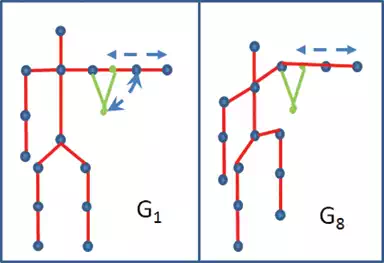
FIGURE 12.
Gestures G1G1 and G8G8. Gesture G1G1 involves a movement in a plane parallel to the camera, whereas gesture G8G8 involves a movement in a plane perpendicular to the camera.
STATISTICAL EVALUATION
The analysis of the performance of the different methodologies, presented above, allows us to draw some important conclusions that must be considered in order to build a robust human‐robot interface. The recognition is highly influenced by the following elements: the subjectivity of the users, the complexity of the gestures, and the recognition performance of the applied methodology. In order to give an overall evaluation of the experimental results, a statistical analysis of the conducted tests has to be done. The F‐score, also known as F‐measure or F1F1‐score, has been considered as global performance metrics. It is defined by the following equation:
![]()
where TPTP, FPFP, and FNFN are the true positives, false positives, and false negatives, respectively. The best values for the F‐score are those close to 1, whereas the worst are those close to 0. This measure captures information mainly on how well a model handles positive examples.
Figure 13 shows the F‐score values obtained for each methodology and for each gesture, averaged over all users. As can be seen each methodology behaves differently among the set of available gestures: SVM, for example, has an F‐score close to 1 for G1 and G8, whereas DNN has maximum F‐score in the case of G2 or G4. Figure 13 highlights another important aspect: some gestures are better recognized instead of others. This is the case, for example of G8 or G4 for which the F‐scores reaches high values whatever methodology is applied. On the contrary, gestures such as G5 or G7 are generally badly recognized by each methodology. These considerations are very useful as allows us to select a subset of gestures and for each of them the best methodology in order to build a robust human robot interface. To this aim, a threshold (=0.85) can be fixed for the F‐score values and the gestures that have at least one classifier with F‐score above this threshold can be selected. By seeing Figure 13, these gestures are: G1,G2,G4,G8,G9, and G10. For each selected gesture the classifier with the maximum F‐score can be chosen: so SVM for G1, DNN for G2 and G4, SVM for G8, DTW for G9, and finally SVM for G10. These set of gestures with the relative best classifiers can be used to build the human‐robot interface.
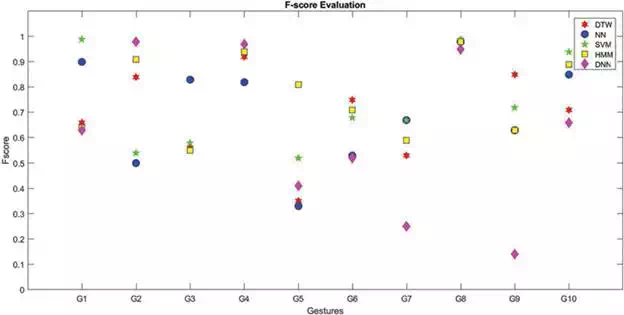
FIGURE 13.
F‐score values of all methodologies for each gesture averaged over all users.
Conclusions
In this chapter the problem of Gesture Recognition has been considered. Different methodologies have been tested in order to analyze the behaviors of the differently obtained classifiers. In particular, neural network (N), support vector machine (SVM), hidden Markov model (HMM), deep neural network (DNN), and dynamic time warping (DTW) approaches have been applied.
The results obtained during the experimental phase prove the great heterogeneity of tested classifiers. In this work, the majority of problems arise in part from the complexity of the gestures and in part from the variations coming from the users. The classifiers perform differently often preserving complementarity and redundancy. These peculiarities are very important for fusion. So, encouraged by these observations, we will concentrate our further investigations on the fusion of different classifiers in order to improve the overall performance and reduce the total error.