Layered Path Planning with Human Motion Detection for Autonomous Robots
Autonomous and intelligent navigation in a dynamic and unstructured environment is a critical capability for mobile robots and autonomous systems. It integrates lots of technologies from sensing, environmental modeling, object tracking, planning, decision making, control, and so on, to deal with the challenges from a dynamic and uncertain environment, so that robots are capable of planning paths to avoid moving obstacles and human beings in a real-world environment.
Lots of researchers have proposed various methods of addressing path-planning problems, which have been applied successfully in various domains. However, most of those methods targeted at finding a path-planning solution in a two-dimensional (2D) environment, or an oversimplified three-dimensional (3D) environment. As more and more mobile robots and autonomous systems are placed in buildings to provide services for human beings, an emerging and interesting problem is how to plan paths for robots to navigate effectively across floors in a multistorey building.
Consider a multistorey building with multiple elevators or escalators on the same floor. If we ask a robot to deliver a box from the first floor to the fifth floor in the building, there will be multiple paths for the robot to navigate via the elevators or the escalators. For example, the robot can take the elevator to go to the fifth floor directly and then go to the destination. Or if the fifth floor is very crowded with people, it can use the elevator on the first floor to go to the second floor, and then go to another elevator at a different location on the second floor to reach the destination on the fifth floor. Then, it becomes a practical and important problem to choose which elevators the robot should take, based on the dynamic environment and human context information.
Additionally, the final state on one floor is the initial state of the next floor, toward which the robot is navigating. While the cost function on each floor can be minimized locally based on some criteria, how to minimize the global cost is also an interesting question that we need to answer. Since there will be people walking in a building, the environment is changing constantly, and thus the cost of moving from one location to another location varies based on timing, business schedule, and other factors. The scenario described above can be extended to other industrial domains, such as transporting in rail yard (multiple 2D environment), health-care service robotics (hybrid 2D environment), and aerial service robotics (full 3D path planning).
The motivation of this chapter is to propose a solution to address the two major problems mentioned above. First, we present a method of building a global graph to describe the environment, which takes human motion in the environment into consideration. Human motion can be detected and its 2D spatial distribution can be estimated by the state-of-the-art radio tomographic imaging (RTI) technology. Then, we use a hidden Markov model (HMM) to represent a long-term context model. In the application stage, when humans are detected, we use the long-term context model to predict the short-term activities of humans in the environment. Then, we build Reactive Key Cost Maps (RKCMs) for all the floors using the predicted human activities.
Second, we present a hierarchy planning framework for robots to find a path to minimize the global cost. This method considers the whole map as a graph, and the adjacent subgraphs for corresponding floors are connected using elevator or stairs, which are also associated with costs. By planning on the higher layer of the global graph, we can optimize the global cost.
The rest of the chapter is organized as follows: Section 2 summarizes previous work on indoor human detection and motion planning, Section 3 explains our methodology in detail, Section 4 uses some experimental results to validate our proposed methodology, and Section 5 proposes some future work and summarized this paper.
Motivation
In a Veteran Affairs (VA) hospital, thousands of surgical tools are transported between the operating rooms and the sterilization facilities every day. Currently, the logistics of the perioperative process is labor intensive, with medical instruments being processed manually by people. This manual process is inefficient and could lead to improper sterilization of instruments. A systematic approach can dramatically improve surgical instrument identification and count, sterilization, and patient safety.
A fully automated robotic system involves multiple mobile and static robots for both manipulation and transportation. The overall robotic system is shown in Figure 1. A key task throughout the sterilization process is to move robots in the hospital from one location to another location while avoiding hitting any obstacles including assets and people. It is a typical indoor robot navigation task. However, due to the dynamic human activities in a hospital, we need to address two challenges: one is to detect and track human motion and activities in the hospital, and the other is to plan the motion trajectories for robots to navigate through multiple floors.
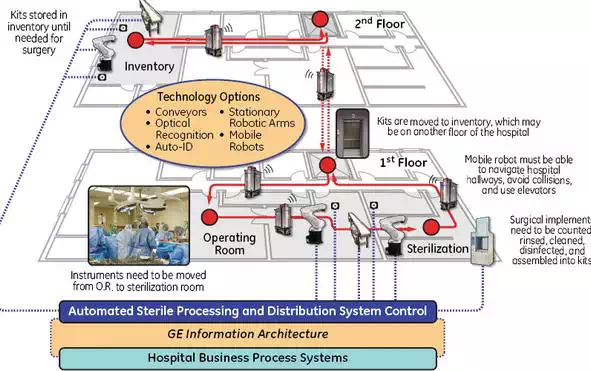
FIGURE 1.
Overall robotic system.
Related work
Robot navigation is one of the most important topics in robotics; many sensors and techniques have been studied in the past few decades [1]. Odometer and inertial sensors such as accelerometer and gyroscope have been used for dead reckoning, that is, relative position estimation. For absolute position measurements, various systems have been developed using sensors such as magnetic compasses, active beacons, and global positioning system (GPS) chips. Combining relative and absolute position measurements, GPS-aided inertial navigation systems have achieved satisfying performance for many outdoor robotic applications. However, accurate and robust localization is still an open problem in the research community for an indoor environment and GPS-denied situation.
As wireless devices and networks become more pervasive, radio-based indoor localization and tracking of people becomes a practical and cost-effective solution. Extensive research has been performed to investigate different wireless devices and protocols such as ultra-wide band (UWB), Bluetooth, Wi-Fi, and so on to locate people carrying radio devices at indoor or GPS-denied environments. A few recent studies even measure and model the effect of the human body on the antenna gain pattern of a radio, and use the model and the effect to jointly track both the orientation and position of the person wearing a radio device such as an radio-frequency identification (RFID) badge. However, all these methods require people to participate in the motion capture and tracking system by carrying devices with them all the time.
With respect to motion planning, there are some existing methods that use the historical human activity data to assist robotic motion planning. A well-known example is the planning engine in the Google Map, which relies on crowd-sourced user data. However, we are targeting on robot motion planning at indoor environments, where we cannot collect human activity data from Google Map or GPS. We also cannot expect that everyone in a building can hold a device for us to collect the human-associate data. A natural and noncooperative method is to obtain such data by actively detecting and tracking human activities in the environment without mounting any sensors on human bodies, and that is the basic innovation point and contribution of our method proposed in this book chapter. The technology we used in this book chapter successfully helps us build a model to describe human activities in the environment.
For robots to interact with human beings, human motion detection and tracking is a critical problem to solve. Recently, a novel sensing and localization technique called radio tomographic imaging (RTI) was developed to use received signal strength (RSS) measurements between pairs of nodes in a wireless network to detect and track people. Various methods and systems have been developed to improve the system performance at different situations. For example, a multichannel RTI system was developed by exploring frequency diversity to improve the localization accuracy. A variance-based RTI (VRTI) was developed to locate and track moving people even through nonmetal walls. Further, to locate stationary and moving people even at non–line-of-sight (NLOS) environments, kernel distance-based RTI (KRTI) was developed that uses the histogram distance between a short-term and a long-term RSS histogram. The state-of-the-art RTI technology has been used to locate and track people in buildings, but we are not aware of any research effort in using RTI to assist human robot interaction and robot path planning.
RTI technology could help us describe human activities in the environment, especially in buildings. The next step is to use appropriate methods to represent the information obtained. When building a model of describing human activities, some researchers focused on building a mathematical field model, for example, Gaussian Mixture Model (GMM). Given a position, the model returns a density of humans in the environment. Some researchers use nodes to represent humans. One well-accepted and popular method is hidden Markov model (HMM). Both discrete and continuous HMMs have been proposed to describe states and transitions. In our system, we choose to use discrete HMM to simplify the model and reduce the computing time when the robot is moving. Lots of literatures can be found in this paper for using HMMs in robotics research. In our method, we used HMMs, but we describe human activities using the costs, not the nodes. Our contribution is to successfully integrate the human detection results into an HMM and reduce the number of nodes in the HMMs for robotic path planning.
Based on the representation model that we chose, a motion-planning algorithm is used to enable robots to find a path from the current location to the target position by searching the reachable space and finding a path to satisfy task constraints. The path-planning process can be done in a configuration space or a task space. Current path-planning methods are categorized into three types: (1) roadmap, which samples the configuration of a task space and finds a shortest or an optimal path to connect the sampled points; (2) potential field, which generates a path in the configuration or a task space by moving a particle attracted by the goal and repelled by impedance areas; and (3) strategy searching, which searches the policy or strategy database to find a solution that describes the path.
Methodology
The proposed system includes several subsystems such as robot navigation, human activity and motion detection, long-term context model, and so on. The overall system architecture is shown in Figure 2. We explain each subsystem in detail in this section.
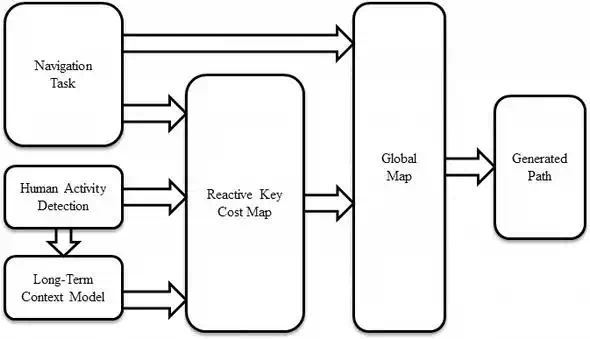
FIGURE 2.
System architecture.
First, we need to detect human activities in the environment. The detection result is used for building a long-term context model in the learning stage and predicting the current human activities in the environment in the application stage. Most of human activities could be simplified as human motions and locations if we do not want to consider what humans are doing. In the human detection part, we choose to use the KRTI technology to record the locations of humans in the environment. The locations are recorded together with timing information to construct a hidden Markov model, which is stored as our long-term context model, after the model is learnt and built. In the application stage, whenever a human is detected in the environment, robots use the context model to predict the human’s activity in the future a few minutes/hours depending on the use cases. The descriptions of current and predicted humans’ activities are combined to generate impedance areas. The impedance areas will be used to generate Reactive Key Cost Maps describing the cost between the key locations including elevators and the stairs. All the RKCMs are connected by elevators and stairs, where robots can use to move from one floor to another. The connected graph is the global graph describing the current paths and connections in the multifloor environment.
When a target is defined in the cost map, which does not belong to elevators and the stairs, we add the target location to the graph and use a Gaussian model to compute the cost of moving from key locations to the target location. The robot then tries to search a shortest path from its current location to the target location in the global graph. Please notice that the path maps are changing all the time, because the information on the heat map changes continuously based on the current and predicted human activities, which are detected by our indoor localization sensors.
HUMAN MOTION AND ACTIVITY DETECTION
This part is the first step of the whole system. All the following analysis, planning, and decision making are based on the detection results coming from this step. The input of this step is the locations detected by the sensors, and the output of this step is different in the learning stage and the application stage. In our system, we propose to use kernel distance-based radio tomographic imaging (KRTI) to detect human beings and track their positions in the environment. First, we give a simple introduction to the KRTI system.
Assume we have a wireless network with L links. For each link, received signal strength (RSS) is measured at the receiver from the transmitter, and we use ql to denote the histogram of the RSS measurements recorded during a calibration period, and use pl to denote the RSS histogram in a short time window during the online period. Then, we can calculate the kernel distance between two histograms ql and pl for each link as
![]()
where K is a kernel matrix from a kernel function such as a Gaussian kernel.
Let d=[d0,⋯dL−1]T denote a kernel distance vector for all L links of a wireless network, and let x=[x0,⋯,xM−1]Tdenote an image vector representing the human motion and presence in the network area. Then, the previous RTI work has shown the efficacy of a linear model W to relate RSS measurements with the image vector x :
![]()
where n is a vector representing the measurement noise and model error.
Finally, a KRTI image xˆcan be estimated from the kernel distance vector d using the generalized least-squares solution :
![]()
where Cx is the covariance matrix of x, and Cn is the covariance matrix of n. More details of the KRTI formulation can be found in Ref.
In the learning stage, the goal is to build a heat map describing long-term human activities. The process is to put the sensor in the environment for a long and meaningful time and record the human locations with temporal information. In our experience, the duration of this process depends on the situational environment and the requirements of applications. Normally, we put the sensors in the environment for one whole week to collect weekly based data. The reason is that we find the daily human activities to be largely different and the weekly human activities have some trackable patterns. Figure 3 displays an example of detected human activities in a small environment.
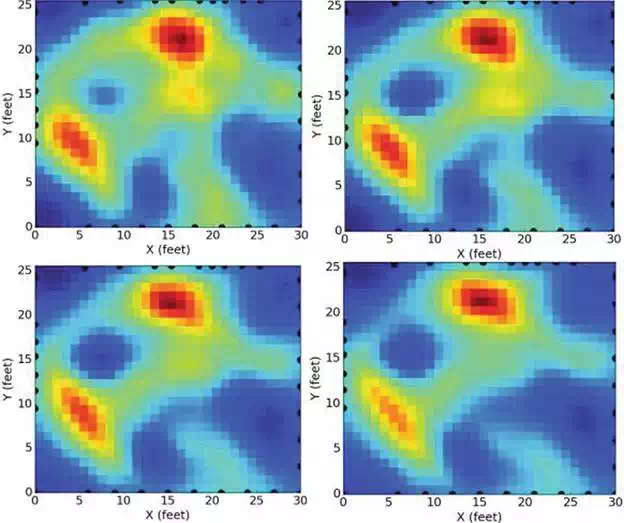
FIGURE 3.
Human motion detection.
To simplify the modeling process, we use Gaussian Mixture Model (GMM) to model the locations. The ‘hot’ locations are described as Gaussian models whose centers are the peak points of activities that happen every day. It is easy to understand that those peak points are some public spaces in the environment. Mathematically, the location of each Gaussian model is described as
![]()
where k represents the kth floor, j is the index number of the Gaussian model on the kth floor, (x, y) is the location of the center of the Gaussian model w.r.t. the local coordinates of the kth floor, and σ is the variance.
Then, based on the temporal information, a Hidden Markov Model can be built. The HMM model describes the relationship between each location, especially when a human is within an area described using Gaussian model, where he/she will move to.
Assuming on kth floor, we have N Gaussian models and is monitored from the starting time: t1, and the current state qt is Si at time t. The probability of the transition from qt = Si to qt+1 = Sj at time t + 1 is
![]()
The state transition matrix is defined as A, where
![]()
Then, the observation matrix defined as B is given by
![]()
It means that the measured value is vk at time t while the current state is Gk(i).
The initial state distribution is defined as
![]()
The complete Hidden Markov Model then is defined as
![]()
Then, this model describes the transition between two locations based on the observations. As mentioned in Ref., the Bayesian method is used to determine the number of states in a HMM model by minimizing the equation:
![]()
where Lf is the likelihood of the model given the observed demonstration, np is the number of the independent parameters in the model, and T is the number of observations. The model, which has the smallest value according to Eq. (10), will be chosen.
An example of a HMM built for our system is shown in Figure 4.
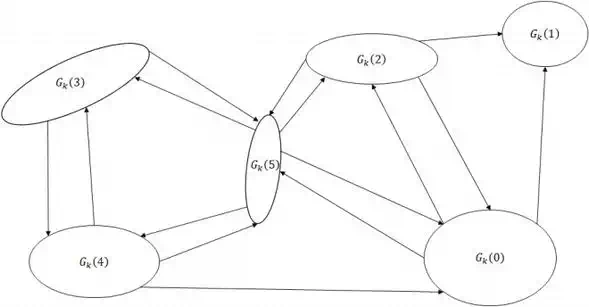
FIGURE 4.
Example of HMM of human activities.
Given an observation Ok, the nearest Gaussian model is computed:
![]()
which is used to define the current state Gk(i).
The most probable area where the human will move to is determined by the equation:
![]()
then the area covered by Gk(l) and Gk(m) will be masked as high-impedance area in the map in the next step.
One important thing we want to mention is that there are lots of people moving in a business building. Then from the detection side, there will be lots of areas masked as high-impedance areas.
REACTIVE KEY COST MAP
After we have the high-impedance areas obtained from the application stage of human activity detection, the next step is to use a map or a graph, which is associated with costs between two key locations, to describe the current environmental information. In our method, Gaussian models are used to describe human activities at hot locations in the environment. However, we do not need to use all of them in the global shortest path searching. What we care about is the cost between key locations, not all the locations. The key locations in our definition are (1) elevators and stairs, which connect two floors and (2) target locations, which may not be the hot locations we detected in the above sections but the robot needs to move to.
We segment the free space of a static map into grids. Then, we overlay the high-impedance areas to the static grid-based map as shown in Figure 5.
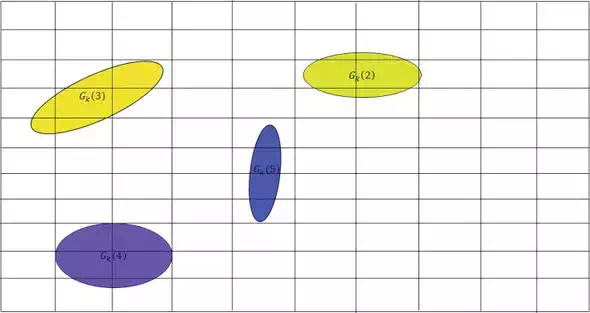
FIGURE 5.
Map overlay.
The cost of moving from one grid to an adjacent free grid is always 1, and the cost of moving from one grid to an adjacent impedance grid is defined using the following equation:
![]()
impedancecurrent is defined by the number of people. And impedancehistory is defined by the number of people detected at t from the historical data.
Using c(i, j), we can build a Reactive Key Cost Map for each floor. As we mentioned earlier, we do not care about the path between each location, but it is necessary to find the cost of paths between key locations.
However, most of the time, a target location in a navigation task is a public space like a conference room, an office, and so on, which are not close to the key locations. So before we build our cost graph, we need to build one additional key location in the map. Then, we connect the closest neighbors to the target node. The cost is computed using the Gaussian impedance area:
![]()
where x is the target location, xi is the center of the Gaussian impedance area, and Σ is the variance matrix. Figure 6 displays the cost map generated from Figure 5.
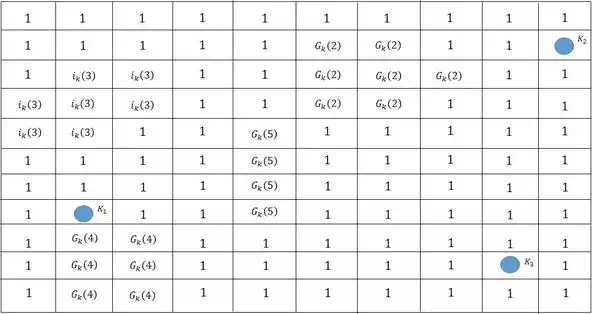
FIGURE 6.
Cost map with three key points.
Then, we apply a shortest path-searching algorithm to find the shortest paths between all the key locations on each floor. In our system, we used A* algorithm, since the map is known and the heuristic and current cost are all known. Specifically, A* selects the path that minimizes
![]()
where n is the last node on the path, g(n) is the cost of the path from the start node to n, and h(n) is a heuristic that estimates the cost of the cheapest path from n to the goal.
After the searching, a Reactive Key Cost Map is built and all the paths are described with cost, which is shown in Figure 7.
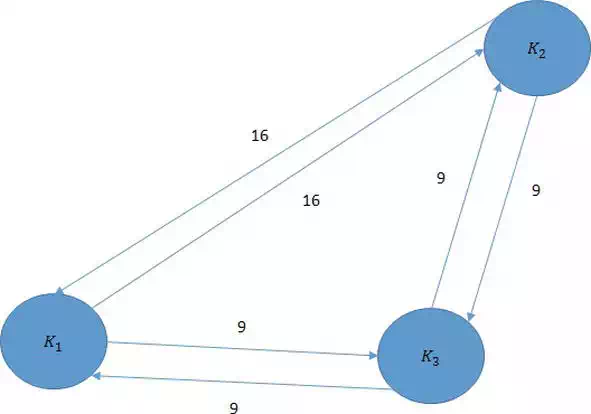
FIGURE 7.
Example of Reactive Key Cost map.
The next step is to connect all the maps of floors together and the connection points are elevators and stairs. This is a simple matching and connection process.
PATH SEARCHING
After the maps of the whole building is built, path searching and planning can all be done in the global map.
Since we largely reduce the complexity of the map by building a Reactive Key Cost Map, the computing task on the path-searching part is not very difficult. We use Dijkstra’s algorithm to find a shortest path in a constructed directed map. Dijkstra’s algorithm is a greedy searching algorithm to find a shortest path in a directed graph by repeatedly updating the distances between the starting node and other nodes until the shortest path is determined. Let the node at which we are starting be called the initial node. Let the distance of node Y be the distance from the initial node to Y. Dijkstra’s algorithm will assign some initial distance values and will try to improve them step by step as follows:
1. Assign to every node a tentative distance value: set it to zero for our initial node and to infinity for all other nodes.
2. Mark all nodes unvisited. Set the initial node as current. Create a set of the unvisited nodes called the unvisited set consisting of all the nodes except the initial node.
3. For the current node, consider all its unvisited neighbors and calculate their tentative distances. For example, if the current node A is marked with a distance of six, and the edge connecting it with a neighbor B has length 2, then the distance to B (through A) will be 8, the summation of the above two numbers. If this distance is less than the previously recorded tentative distance of B, then overwrite that distance. Even though a neighbor has been examined, it is not marked as “visited” at this time, and it remains in the unvisited set.
4. When we are done considering all the neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again.
5. If the destination node has been marked visited (when planning a route between two specific nodes) or if the smallest tentative distance among the nodes in the unvisited set is infinity (when planning a complete traversal), then stop. The algorithm has finished.
6. Select the unvisited node that is marked with the smallest tentative distance, and set it as the new “current node,” then go back to step 3.
Using Dijkstra’s algorithm, in a map, a shortest path can be generated from the “Starting” node to a destination node. In our testing, we found some issues when applying Dijkstra’s algorithm in 3D path searching. Then, we simplify our case by confining that the global map can be represented as a 2D graph. This paper does not focus on proposing a novel planning algorithm, so improving the motion-planning algorithm is not the concentration.
Experiments and results
To evaluate our system, we need to have two types of evaluation. One is to make sure the path can be generated. We tested this part in a static environment assuming that the human motion and activities have been detected and remained the same for a certain amount of time. The second testing is to test the reactive planning. Assuming that humans are moving in the environment, then we generate a path plan reactively based on the current environmental situation. This part is to validate that the system is responsive quickly enough to deal with the uncertain and unexpected human activities in the environment. First, we describe how we perform experiments to evaluate our human motion-tracking system.
HUMAN DETECTION RESULTS AND DATASET OF RTI LOCALIZATION
We use the TelosB motes as our wireless nodes to form a wireless network as our testbed. We deploy nodes at static locations around an area of interest, as shown in Figure 8. All nodes are programmed with TinyOS program Spin so that each node can take turns to measure the received signal strength from all the other nodes. A base station is connected to a laptop to collect pairwise RSS measurements from all nodes of the wireless network. Once we collect RSS from the network, we feed the RSS vector to our KRTI formulation as described in Section 4.1.1.
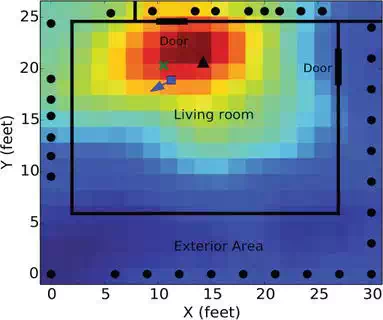
FIGURE 8.
Experimental layout with reconstructed RTI image (anchor nodes shown as bullets, true person position shown as a cross, RTI position estimate shown as a triangle, and robot’s orientation and position are shown as arrow and square for illustration purpose).
We describe our experiment in a controlled environment to evaluate our motion-tracking system. As shown in Figure 8, 34 TelosB nodes were deployed outside the living room of a residential house. Before people started walking in the area, we collect pairwise RSS measurements between anchor nodes as our calibration measurements. During the online period, people walked around a marked path a few times in the living room, so that we know the ground truth of the locations of the people to compare with the estimate from RTI. The reconstructed KRTI image is shown in Figure 8 with the black triangle indicating the location of the pixel with the maximum pixel value, which is the location estimate of a person. Note that KRTI can detect human presence by choosing a threshold of the pixel value based on the calibration measurements. KRTI is also capable of tracking multiple people, as shown in Figure 3. More details of the experiments and dataset can be found in Refs.
SIMULATION RESULTS
We tested our proposed algorithm in simulation. After detecting the human activities, the robot builds the heat map and the 2D RKCM of each floor. Figure 9 displays three 2D graphs of three floors, which are labeled by shadowed circles. They are connected by stairs or elevators. The cost of moving from one floor to another floor using the elevators or stairs is manually defined as three in our graphs.
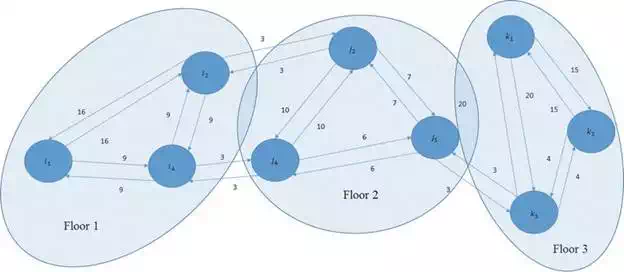
FIGURE 9.
Reactive Key Cost map.
The distance matrix used for Dijkstra’s searching algorithm is shown in Eq. (16). Each row represents the distance from one node to other nodes. The elements represent the distance values. Given a task of the start point i1 on map 1 and the goal state k3 on map 3, the robot finds a path from i1 to k3 as shown in Figure 10. The cost of the path is 25 which is the global minimum cost.
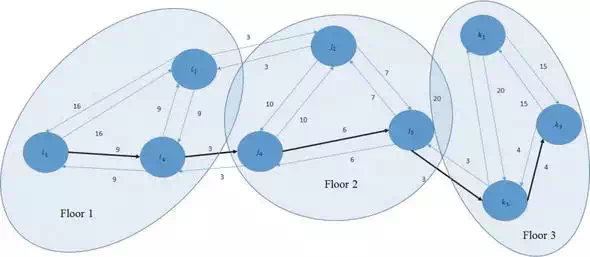
FIGURE 10.
Experimental results.
Comparing the time spent on movement and detection, the time of finding path based on RKCM can almost be ignored. There are lots of papers describing the algorithm complexities of Dijkstra’s algorithm and other algorithms, where readers can refer to

We still use traditional online sense-plan-act algorithms when the robot is moving. However, the experiments here largely reduce the computing workload on the robot side. The robot knows in advance what is happening in the environment based on the HMM model built from historical data, then it uses the HMM to find a path which is optimal based on the historical information, under the assumption that the current situation is similar to the historical situation during the same time every day or every week.
DISCUSSION
From the above experimental results, we can clearly see that our system builds the global graph using the monitored human activities and generates a shortest path for robots to move to the target locations.
In most indoor robotic navigation challenges, especially in crowded environment, researchers tend to equip robots with various sensors to make sure that they can detect everything in the environment. Then based on the comprehensive detection and recognition process, a smart decision-making mechanism can help robots to plan the motion, switch strategies, and move freely in the environment. This method enforces large workload on the online-computing component. The motivation of this book chapter is to find a method to reduce such workload based on historical data of human motion and activity.
Based on the collected human activity data, we use a simple HMM to describe the cost of movement in the environment. Then, robots can plan the motion in advance to avoid moving to a very crowded area. We have seen lots of cases that robots run into a crowd of human and have lots of difficulty in moving out of that area, which generates concerns on safety, cost, and efficiency. Our method can avoid such a situation based on the modeling results as seen from the last section.
We do find some situations that the system does not work very well. When the robot moves too fast, and the humans nearby are walking, the planning is not fast enough to reflect the current changes of the environment, and thus collision happens. We have not done much testing on this part and we plan to have more testing to make the system more robust in such situations.
Additionally, we cannot expect that static HMM model can provide satisfying information for robots to use. Every day, new patterns of human activities may appear in the environment and the model needs to be updated accordingly. Thus, it is desirable to perform data collection and modeling when robots are moving, which enables robots to have the lifelong learning capability. This capability could help robots to have up-to-date information to use and make the planning more efficient and useful.
Moving one robot in a building is challenging, but motion planning for a group of robots is even more complex [35, 36]. Sharing latest updated human activity models among robots is key to the success to realize coordinated and collaborated robotic motion planning. The critical technical problem is to design a method of fusing models into one for all the robots to use.
Conclusion
This book chapter proposes a hybrid method of planning paths in a global graph composed of subgraphs. We take the human activity into consideration to build a cost graph. This method significantly reduces the computing workload because it avoids planning in a global graph with lots of grids and possibilities. We also carry out experiments in simulation to validate our proposed method. The methods proposed in this chapter provide a solution to enable autonomous systems/robots to navigate effectively and robustly in human-existing multistorey buildings.