Robust Accelerating Control for Consistent Node Dynamics in a Platoon of CAVs.
The platoon driving of automated connected vehicles (CAVs) has considerable potential to benefit road traffic, including increasing highway capacity, less fuel/energy consumption and fewer accidents. The R&D of CAVs has been accelerated with increasing usage of wireless communication in road transportation, such as dedicated short range communications (DSRC). Pioneering studies on how to control a platoon of CAVs can date back to 1990s, and as pointed out by Hedrick et al. , the control topics of a platoon can be divided into two tasks: (1) to implement control of platoon formation, stabilization and dissolution; and (2) to carry out controls for throttle/brake actuators of each vehicle. These naturally lead to a hierarchical control structure, including an upper level controller and a lower level controller. The upper one is to retain safe and string stable operation, whereas the lower one is to track the desired acceleration by determining throttle/brake commands.
The upper level control of a platoon of CAVs has been investigated extensively. An earlier work done by Shladover introduced many known control topics, among which the most famous is the concept of string stability. The string stability ensures that range errors decrease as propagating along downstream. Stankovic et al. proposed a decentralized overlapping control law by using the inclusion principle, which decomposes the original system into multiple ones by an appropriate input/state expansion. Up to now, many other upper level control topics have already been explored, including the influence of spacing policies, information flow topologies, time delay and data loss of wireless communications, etc.
The lower level controller determines the commands for throttle and/or brake actuators. The lower level controller, together with vehicle itself, actually plays the role of node dynamics for upper level control. Many research efforts have been attempted on acceleration control in the past decades, but still few gives emphasis on the request of platoon level automation. Most platoon control relies on one critical assumption that the node dynamics are homogeneous and approximately linear. Then, the node dynamics can be described by simple models, e.g. double-integrator and three-order model. This requires that the behaviour of acceleration control is rather accurate and consistent, which is difficult to be achieved. One is because the salient non-linearities in powertrain dynamics, both traditional and hybridized, and any linearization, will lead to errors; the other is that such uncertainties as parametric variations and external disturbances significantly affect the consistence of control behaviour.
One of the major issues of acceleration control is how to deal with non-linearities and uncertainties. The majority to handle non-linearities are to linearize powertrain dynamics, including exact linearization, Taylor linearization and inverse model compensation. Fritz and Schiehlen use the exact linearization technique to normalize node dynamics for synthesis of cruising control. After linearization, a pole placement controller was employed to control the exactly linearized states. The Taylor expansion approach has been used by Hunt et al. to approximate the powertrain dynamics at equilibrium points. The gain-scheduling technique was then used to conquer the discrepancy caused by linearization. The inverse model compensation is widely used in engineering practice. This method is implemented by neglecting the powertrain dynamics. For the uncertainties, the majority rely on robust control techniques, including sliding model control (SMC), H∞ control, adaptive control, fuzzy control, etc. Considering parametric variations, an adaptive SMC was designed by Swaroop et al. by adding an on-line estimator for vehicle parameters, such as mass, aerodynamic drag coefficient and rolling resistance. Higashimata and Adachi and Yamamura and Seto designed a Model Matching Controller (MMC) based controller for headway control. This design used an H∞ controller as feedback and a forward compensator for a faster response. Xu and Ioannou approximated vehicle dynamics to be a first-order transfer function at equilibrium points, and then the Lyapunov approach was used to design an adaptive thriller controller for tracking control of vehicle speed. Keneth et al (2008) designed an adaptive proportional-integral (PI) controller for robust tracking control in resistance to parametric variations. The adaptive law is designed by using the gradient algorithm. The aforementioned robust controllers are useful to resist small errors and disturbances in vehicle longitudinal dynamics, but might not be always effective for large uncertainties. Moreover, the use of adaptive mechanism is only able to resist slowly varying uncertainties, but difficult to respond fast varying disturbances, e.g. instantaneous wind.
Node dynamic model for control
This chapter proposes a robust acceleration control method for consistent node dynamics in a platoon of CAVs. This design is able to offer more consistent and approximately linear node dynamics for upper level control of platoons even under large uncertainties, including vehicle parametric variation, varying road slop and strong environmental wind. The controlled node in the platoon is a passenger car with a 1.6 L gasoline engine, a 4-speed automatic transmission, two driving and two driven wheels, as well as a hydraulic braking system. Figure 1 presents the powertrain dynamics. Its inputs are the throttle angle αthr and the braking pressure Pbrh. Its outputs are the longitudinal acceleration a, vehicle velocity v, as well as other measurable variables in the powertrain. When driving, the engine torque is amplified by the automatic transmission, final gear, and then acts on two frontal driving wheels. When braking, the braking torque acts on four wheels to dissipate the kinetic energy of vehicle body.
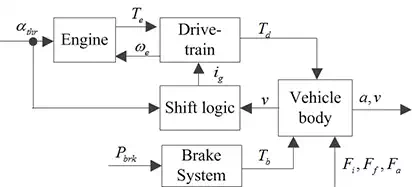
FIGURE 1.
Vehicle longitudinal dynamics.
VEHICLE LONGITUDINAL DYNAMICS
For the sake of controller design, it is further assumed that (1) the dynamics of intake manifold and chamber combustion are neglected, and overall engine dynamics are lumped into a first-order inertial transfer function; (2) the vehicle runs on dry alphabet roads with high road-tyre friction, and so the slip of tire is neglected; (3) the vehicle body is considered to be rigid and symmetric, without vertical motion, yaw motion and pitching motion; (4) the hydraulic braking system is simplified to a first-order inertial transfer function without time delay. Then, the mathematical model of vehicle longitudinal dynamics is
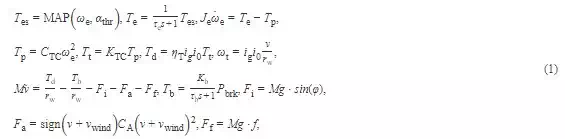
where ωe is the engine speed, Tes is the static engine torque, τe is the time constant of engine dynamics, Te is the actual engine torque, MAP(.,.) is a non-linear tabular function representing engine torque characteristics, Tp is the pump torque of torque converter (TC), Je is the inertia of fly wheel, Tt is the turbine torque of TC, CTc is the TC capacity coefficient, KTC is the torque ratio of TC, ig is the gear ratio of transmission, io is the ratio of final gear, ηT is the mechanical efficiency of driveline, rw is the rolling radius of wheels, M is the vehicle mass, Td is the driving force on wheels, Tb is the braking force on wheels, v is the vehicle speed, Fi is the longitudinal component of vehicle gravity, Fa is the aerodynamic drag, Ff is the rolling resistance, Kb is the total braking gain of four wheels, τb is the time constant of braking system, CA is the coefficient of aerodynamic drag, g is the gravity coefficient, f is the coefficient of rolling resistance, ϕ is the road slope and vwind is the speed of environmental wind. The nominal values of vehicle parameters are shown in Table 1.
INVERSE VEHICLE MODEL
One major challenge of acceleration control is the salient non-linearities, including engine static non-linearity, torque converter coupling, discontinuous gear ratio, quadratic aerodynamic drag and the throttle/brake switching. These non-linearities can be compensated by an inverse vehicle model. The inverse models of engine and brake are described by Eqs. (2) and (3), respectively [22, 31]. The design of the inverse model assumes that (i) engine dynamics, torque converter coupling, etc. is neglected; (ii) vehicle runs on dry and flat road with no mass transfer; (iii) the inverse model uses nominal parameters in Table 1.
![]()
![]()
where ades is the input for the inverse model, which is the command of acceleration control, Tedes, αthrdes, Fbdes and Pbrkdes are corresponding intermittent variables or actuator commands. Note that throttle and braking controls cannot be applied simultaneously. A switching logic with a hysteresis layer is required to determine which one is used. The switching line for separation is not simply to be zero, i.e. ades = 0, because the engine braking and the aerodynamic drag are firstly used, and followed by hydraulic braking if necessary. Therefore, the switching line is actually equal to the deceleration when coasting, shown in Figure 2. The use of a hysteresis layer is to avoid frequent switching between throttle and brake controls.
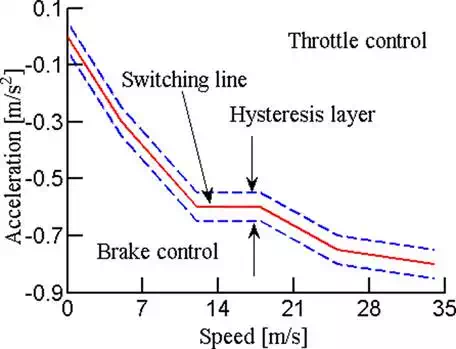
FIGURE 2.
Switching between throttle and brake controls.
MMS-based acceleration control
The Multi Model Switching (MMS) control is an efficient way to control plants with large model uncertainties and linearization errors, especially sudden changes in plant dynamics [27–30]. The overall range of plant dynamics is covered by a set of models instead of a single one, and then a scheduling logic switches the most appropriate controller into the control loop. The speed of adaptation and transient performance can be significantly improved by the instantaneous switching among candidate controllers [29, 30]. Another benefit of MMS control is its potential to enclose the input-output behaviours to a required small range. Figure 3 shows the MMS control structure for vehicle acceleration tracking, where ades and a are the desired and actual longitudinal acceleration respectively, αthrdes and Pbrkdes are throttle angle and braking pressure respectively, which are the control inputs of a vehicle. It consists of the vehicle itself (V), the inverse model (I), a supervisor (S) and a controller set (C). The inverse model I is used to compensate for the non-linearities of powertrain; I and V together constructs the plant for MMS control. The combination of I + V tends to have large uncertainties, but is divided into small ones under the MMS structure. Such a configuration is able to maintain a more accurate and consistent input–output behaviour even under a large model mismatch.
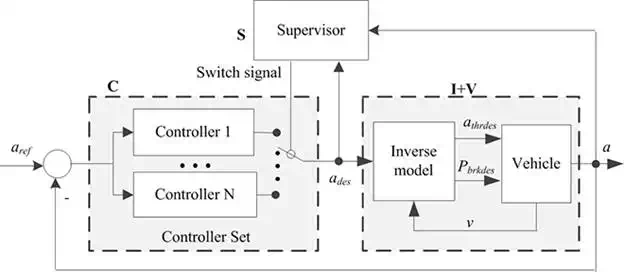
FIGURE 3.
MMS control of vehicle acceleration.
MODEL SET TO SEPARATE LARGE UNCERTAINTY
 .
.
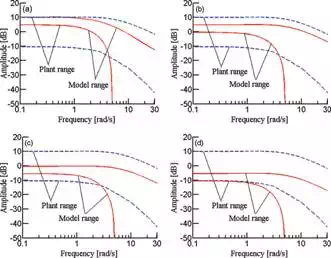
FIGURE 4.
Frequency responses of four linear models. (a) Model P1(s), (b) Model P2(s), (c) Model P3(s) and (d) Model P4(s).
The model set P={Pi(s),i=1,⋯,N}is defined to have identical structure with a multiplicative uncertainty:
![]()
where Gi(s) is the nominal models listed in Table 2, W(s) is the weight function for uncertainty, Δi is the model uncertainty, satisfying:
![]()
where ∥⋅∥δ∞∥ is the induced norm of Lδ2 norm of signals expressed as

where δ>0δ>0 is a forgetting factor, and x(t) is a vector of signals.
|
No. |
1 |
2 |
3 |
4 |
|
Gi(s) |
8.15s+3.333 |
4.5s+3.333 |
0.75s+3.333 |
0.22s+3.333 |
TABLE 2.
Nominal models of node dynamics.
SYNTHESIS OF THE MMS CONTROLLER
The main idea of this chapter is to use multiple uncertain models to cover overall plant dynamics, and so the large uncertainty is divided into smaller ones. Because the range of dynamics covered by each model is reduced using multiple models, this MMS control can greatly improve both robust stability and tracking performance of vehicle acceleration control. This MMS controller includes a scheduling logic S, multiple estimators E and multiple controllers C. The module E is a set of estimators, which is designed from model set P and to estimate signals a and z. Note that z is the disturbance signal arising from model uncertainty and it cannot be measured directly. The module S represents the scheduling logic. Its task is to calculate and compare the switching index of each model Ji(i=1,⋯,N), which actually gives a measure of each model uncertainty compared with current vehicle dynamics. S chooses the most proper model (with smallest measure) and denoted as σ. The module C contains multiple robust controllers, also designed from P. The controller whose index equals σ will be switched into loop to control acceleration. The signal aref is the desired acceleration.
The scheduling logic is critical to the MMS controller, because it evaluates errors between current vehicle dynamics and each model in P, and determines which controller should be chosen. The controller index σ is determined by:
![]()
Intuitively, Ji(t) is designed to measure the model uncertainty σt, and so the estimator set E={Ei,i=1,⋯,N} is designed to indirectly measure σi as follows:

where Λ(s) is the common characteristic polynomial of E, aˆia^i and zˆiz^i are the estimates of a and z using model Pi. It is easy to know that the stability of estimators can be ensured by properly selecting Λ(S). Subtracting Eq. (8) with Eq. (4) yields the estimation error of a:
![]()
Then, the switching index Ji(t) is designed to be
![]()
Since the system gain from zˆσ(t) to eσ(t) can be bounded by S, zˆσ(t) and eσ(t) can be treated as the input and output of an equivalent uncertainty. Considering Eq. (8), E is rewritten into
![]()
where AE,BE1,BE2,CE11,CE12,CE13,CE14,CE21,CE22,CE23,CE24 are matrices with proper dimensions. By selecting weighting function as Wp(s)=(0.1s+1.15)/s, the required tracking performance becomes:
![]()
where aref is the reference acceleration, q=Wp(s)ea and ea=aref−a, which is expected to converge to zero. Substituting a=aˆσ−eσ and Eq. (12) to Eq. (11), we have,
![]()

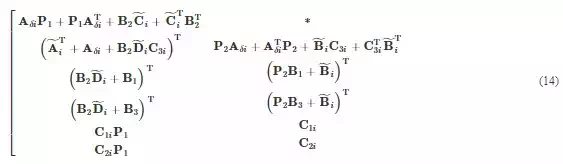

where β < 1 is a positive constant, Aδi=Ai+0.5δI, symbol “*” represents the symmetrical part. Then the controller set C is
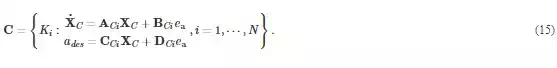
The matrices in Eq. (15) are calculated as:
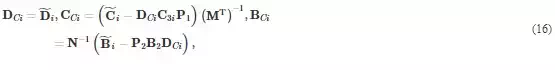
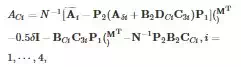

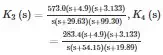
Simulation results and analyses
To validate the improvements MMS controller for tracking of acceleration, two other controllers are designed, i.e. a sliding mode controller (SMC), and a single H∞ controller.
DESIGN OF SMC AND H∞ CONTROLLERS
It is known that SMC has high robustness to uncertainties. It is designed based on the nominal model GM(s)=0.33/(s+0.33). The sliding surface is selected to be
![]()
where λ>0. The reaching law is designed to be ṡ =−ks+ηsgn(s), where k < 0 and η>0. Then the sliding mode controller is
![]()
H∞ control is another widely used and effective approach to deal with model uncertainties. Here, a model matching control structure is applied to balance between robustness and fastness. The uncertain model of vehicle dynamics used for design of H∞ controller is

The referenced acceleration response dynamics is GM(s)=1/(s+1). Then, the feed-forward controller designed by the model matching technique is
![]()
The feedback controller designed by the H∞ control method is

This H∞ controller is numerically solved by the Matlab command mixsyn(), with the weighting function Wp(s)=(0.1s+1.15)s−1.
SIMULATIONS AND ANALYSES
A naturalistic acceleration from real traffic flow is used as the reference acceleration. This naturalistic acceleration profile is from driver experiment data, which lasts around 50 min totally and is shown in Figure 5. The maximum and minimum desired acceleration is about 1.1 m/s2 and −1.8 m/s2, respectively and the vehicle speed varies in the range of 0–33 m/s. This condition can cover a wide range of vehicle dynamics.
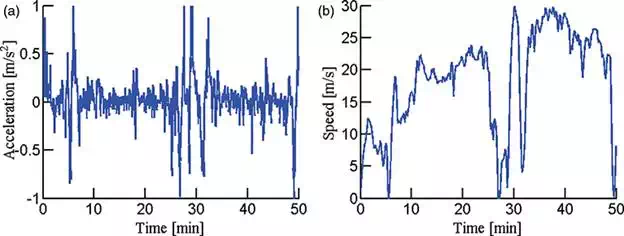
FIGURE 5.
Reference acceleration and speed. (a) Acceleration and (b) Vehicle speed.
Two groups of simulations are conducted: (a) nominal condition; and (b) uncertain condition. Under the nominal condition, all vehicle parameters are shown in Table 1 and there is no road slope and wind. Under the uncertain condition, the disturbed parameters are vehicle mass, road slope and wind. The maximum value of vehicle mass is used, i.e. M = 1600 kg. The disturbance of road slope is a sinusoidal signal:
![]()
where φmax = 5 deg, and Tslope = 50 sec. The disturbance of wind is a periodic triangular signal:
![]()
where vwmax = 10 m/s, and Twind = 40 sec.
The simulations results are shown in Figures 6 and 7, and to show clearly, only the responses from 0 to 500 sec are plotted as a demonstration. From Figure 6(a) and (b), under the nominal condition, all three controllers can track the reference acceleration accurately. With the uncertainties, it is found that from Figure 7(a) and (b) the tracking capability of SMC and H∞ controller decreases obviously while MMS can still ensure acceptable tracking error. Though switching of controller occurs at both nominal and uncertain conditions (Figure 6(e) and Figure 7(e)), the control input of MMS behaves continuously and there is no obvious sudden change (Figure 6(c) and Figure 7(c)). Another concern that must be explained is the spike of acceleration shown in Figure 6(b) and Figure 7(b). This is mainly caused by the impact of powertrain when gear switches. A more appropriately designed transmission model could improve the gear-shifting quality.
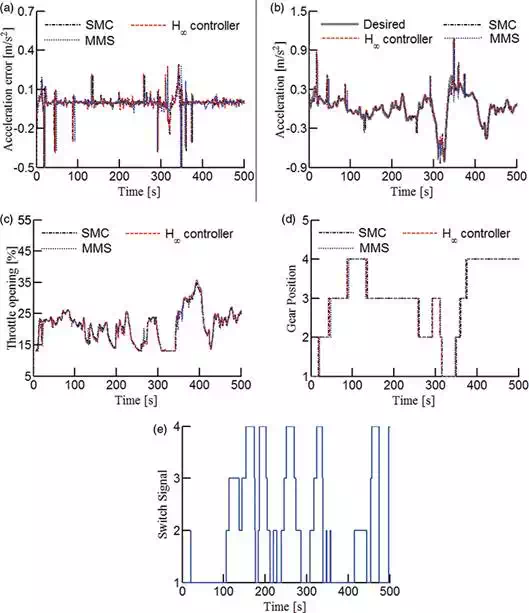
FIGURE 6.
Results under normal condition. (a) Acceleration tracking error, (b) acceleration, (c) throttle control, (d) gear position and (e) switching signal.
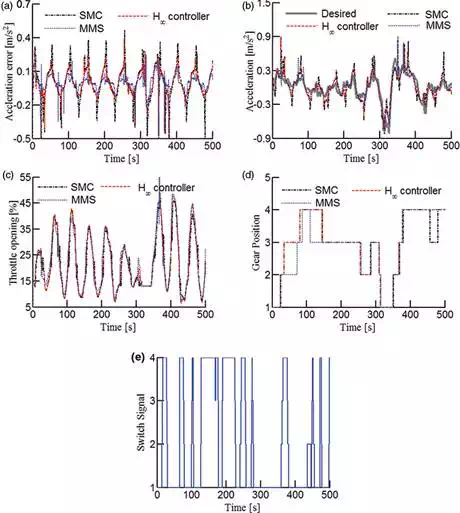
FIGURE 7.
Results under disturbed condition. (a) Acceleration tracking error, (b) acceleration, (c) throttle control, (d) gear position and (e) switching signal.
A more deep simulation is conducted to analyse the influences of uncertain level on the tracking ability of acceleration and gear shifting behaviours. At this condition, the level of uncertainty is increased step by step and the relationship between the uncertain level and model uncertainties is described by:
![]()
where ε represents the level of uncertainty, with maximum mass 1600 kg, maximum road slope 10 deg, and maximum wind speed 20 m/s (when ε = 10). ε = 0 implies that there is no model uncertainty. The root mean square error (RMSE) of acceleration is used to measure the capability of tracking. Figure 8presents the RMSE of acceleration error and the number of gear shifting per minute (denoted as Ngear/min). In nominal condition, the RMSE of acceleration error of the three robust controllers is almost the same. As the uncertainty level increases, the tracking capability of the SMC and H∞H∞ quickly drops, whereas the MMS still holds acceptable accuracy. Figure 8(b) is used to release the concern that the MMS might largely increase the number of gear shifting because of its switching structure.
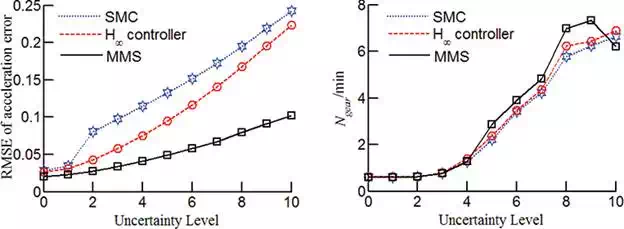
FIGURE 8.
Performances under different uncertain levels.
Conclusions
This chapter proposes a robust acceleration control method for consistent node dynamics in a platoon of automated connected vehicles (CAVs). The design, which is based on multiple model switching (MMS) control structure, is able to offer more consistent and approximately linear node dynamics for upper level control design even under large uncertainties, including vehicle parametric variation, varying road slop and strong environmental wind. The following remarks are concluded:
1. (1) Homogeneous and linear node dynamics is important for platoon control. This requires the acceleration tracking performance to be accurate and consistent, and accordingly results in critical challenges because of the linearization error of powertrain dynamics and large model uncertainties in and around vehicles. The proposed MMS control structure can divide the large uncertainties of vehicle longitudinal dynamics into small ones. Accordingly, multiple robust controllers are designed from the multiple model set, and a scheduling logic is also presented to automatically select the most appropriate candidate controller into loop according to the errors between current vehicle dynamics and models.
2. (2) The designed switching index can measure the model error of vehicle longitudinal dynamics properly and the right acceleration controller is selected into the closed loop. The robust stability and performance of this acceleration tracking control system can be ensured. Both the simulation and experiment results demonstrate that this switching control system has better performances than that designed by either H∞H∞ control or sliding mode control approach in large uncertain conditions.