Application of Sampling-Based Motion Planning Algorithms in Autonomous Vehicle Navigation.

As information technology and artificial intelligence develop rapidly, it is becoming possible to use computers to assist daily driving, even to make the driving process entirely autonomous. Due to the recent research advances in robotics and intelligent transportation systems, autonomous vehicles have attracted dramatic attentions in the past decades.

An important milestone has been reached in the field of autonomous driving on the urban road, which can be seen in DARPA Urban Challenge (DUC). As an important achievement in the progress of autonomous vehicle, the suggested vehicle navigation systems in DUC have been well accepted as the instruction for the design process of autonomous vehicle systems. The majority of the available architectures for autonomous vehicle focused on autonomous driving in structured roads and unstructured parking environments, and thus the performance of these proposals for more complicated driving scenarios is not clear, and despite interesting solutions for this problem in the literature, it is still a basic challenge to design an efficient motion planner for navigation in dynamic and cluttered environments where high number of obstacles, extensive effects of failure and safety considerations make it even more challenging.

One of the challenging research areas in autonomous vehicle is the development of an intelligent motion planner that is able to guide the vehicle in dynamic changing environments. Motion planning is an essential and fundamental part of autonomous vehicle, which can find solutions for the problem of finding a set of control values or feasible motion states for the vehicle to manoeuvre among obstacles from a given initial configuration towards a final one, taking into account the vehicle’s kinematic and dynamic systems. Furthermore, the traffic regulations and the available information on the geometric structures of roads are also included in the motion planning for autonomous driving.

Motion planning can be considered as one of the basic challenges within robotics sciences which have been studied by many researchers over the past few decades resulting in different algorithms with various specifications. Motion planning for an autonomous vehicle is a procedure to find a path from an initial position to a final state, while avoiding any collision with obstacles. In the simplest form of motion planning problem, which is called the piano mover’s problem, the running time of each algorithm is exponentially the degrees of freedom, which indicates that the path-planning problem is NP-Complete. It is also shown that the motion planner needs memory exponential in the degrees of freedom, which proves that the problem is PSPACE-Complete.

When the environment is not known for the robot, the path planning is called online, local or sensor-based. During the past few decades, online path planning has been a challenging but attractive field for many robotic researchers. In unknown environments, there are two main aspects. First, the motion decisions are based on local information, and second, sensing is contemporaneous to the decision-making process. In this class of path planning, the robot acquires the information via its sensors that could be touch or vision sensors.

The field of sensor-based path planning has been studied by many researchers resulting in various algorithms with different characteristics. One of the earliest and simplest online path-planning algorithms is the Bug algorithm that acquires information from touch sensors and guides the robot to the goal through the boundaries of obstacles. An extension of the classic Bug algorithm is Tangent Bug, which incorporates vision sensor information with the algorithm. A performance comparison between different Bug-like algorithms can be found in. Despite interesting performances of the conventional motion planning methods in robotics, their efficiency in navigation of autonomous vehicle is considerably low due to the complex and unstable dynamics of such systems.

Another well-known class of path-planning algorithms is sampling-based path planning. In this class of algorithms, the only source of information is a collision detector, and hence, there is no need to characterize all possible collision situations. Sampling-based methods operate several strategies for creating samples in free space and for connecting them with collision-free paths in order to provide a solution for path-planning problem. Three of the more popular sampling-based approaches include probabilistic roadmap (PRM), randomized potential fields (RPFs) and rapidly exploring random trees (RRTs). PRM approach finds collision-free samples in the environment and adds them to a roadmap graph. Afterwards, by using a cost function, best samples are chosen in the graph and a simple local path planner is used to connect them together. RPFs approach builds a graph by connecting the local minimums of the potential function defined in the environment. Then, the planner searches this graph for paths. RRTs are specially proposed to deal with non-holonomic constraints and high degrees of freedom. This approach builds a tree by randomly choosing a node in the free space and finding the nearest node in the tree. Next, the planner expands this nearest node in the direction of the random node. Several extension of RRT for solving sensor-based path-planning problems has been proposed. In, a new data structure called sensor-based random tree (SRT) is proposed, which represents a roadmap of the visited area. Similar to the RRT, the SRT is a tree of already visited nodes with a local safe region. The tree is increasingly expanded towards a random direction. An improvement of RRT is proposed in. This method directs the robot in an RRT-derived direction while avoiding collision. In, two heuristics are added to the RRT to handling unknown environments. The first heuristic checks if the goal is reachable from the current position of the robot. The second heuristic tries to avoid the robot from getting close to the obstacles. Despite interesting solutions for this problem in the literature, it is still a basic challenge to design an efficient motion planner for navigation in dynamic and cluttered environments where high number of obstacles, extensive effects of failure and safety considerations make it even more challenging. Due to the interesting advantages and properties of sampling-based motion planning algorithms, they seem to be efficient and powerful tools for autonomous vehicle navigation. In this chapter, a novel motion planning architecture is proposed for autonomous vehicle navigation, which employs recent advances in sampling-based motion planning. The resulted approach is capable of planning safe and efficient motions in different situations such as following the course of the road, overtaking the front vehicle and following the front vehicles while overtaking is not possible. The proposed architecture employs the optimal strategy proposed in RRT* planner to avoid meandering paths. The proposed planner also utilizes a unique low-dispersion strategy to reduce the running time of the planner which is essential in autonomous vehicle navigation. The rest of the chapter is organized as follows. In Section 2, the category of sampling-based motion planning algorithms is summarized. The existing applications of sampling-based planners in autonomous vehicle navigation are reviewed in Section 3. Then, the proposed architecture is introduced in Section 3, supported by the simulation studies in Section 4. Finally, discussion and conclusion is provided in Section 5.

Sampling-based motion planning

Naturally, offline path-planning algorithms need a complete map of the configuration space which usually increases the cost and runtime of the search in most problems. Sampling-based motion planning was proposed to solve navigation queries without trying to construct the map of the entire configuration space. Instead, they only depend on a procedure that decides on whether a given configuration of the robot is in collision with obstacles or not. The available sampling-based path-planning algorithms can be categorized into two main classes, namely, roadmap-based or multi-query algorithms and tree-based or single-query algorithms. Roadmap-based algorithms are normally applicable in multi-query scenarios as they form a graph that later will be used to solve different navigation problems. The graph is the main structure used for saving the environmental information, where the nodes represent different configurations in the robot’s configuration space. An edge exist between any two configurations if the corresponding geometrical properties satisfy a set of conditions such as vicinity, and the autonomous agent can navigate from one point to another without any collision. A typical algorithm consists of two main stages: learning or observation stage and search stage. In the first stage, the graph structure is constructed. Collision-free positions or samples are chosen randomly and considered as the vertices of the graph. In the search stage, each vertex is tested to be connected to the closest neighbour configurations, and the resulted successful connection will be an edge in the roadmap. To answer a given planning task, the initial and final configurations are added to the existing graph and a normal search technique is considered for finding the shortest path. The most important factor in the efficiency of the algorithm is how effectively the roadmap can learn the free-space connectivity of the configuration space. In addition, the main problem in the performance of such algorithm is the construction of the graph because the search algorithms usually perform satisfactory in terms of speed and runtime. The original form of PRM planner consists of the following steps. First, a random configuration is selected from the configuration space and is tested if it lies in the free configuration space. If the sample passes this, it will be included in the roadmap structure as a vertex or a node. Second, a search technique takes place to find the closest neighbours in the graph to the new node. Finally, a local planner attempts to connect the closest neighbour and the new configurations based on criteria posed by the planning query. This connection will be added to the graph as a new edge if it is collision free. In several situations, quickly finding a solution for a particular problem is the main objective. In these situations, single-query algorithms can be implemented. In these algorithms, the base of the data structure is normally a tree. The basic idea is to find an initial configuration (the starting configuration) that is the root of the tree and all incrementally generated configurations will be connected to other configurations already included in the tree. The initial tree-based algorithm is the rapidly exploring random tree (RRT) planner. Started to grow from the start configuration, a tree continuously grows in the free configuration space until it gets close enough to the final configuration. An essential feature of this planner is that configurations with larger Voronoi regions (i.e. the part of the free configuration space that is closer to that node than to other members of the tree) have higher chances to be selected in the process of tree expansion. Therefore, the tree normally grows towards yet unknown parts of the environment, circumfusing rapidly in the free configuration space. The initial version of the RRT consists of the following steps. First, a random sample is generated in the free search environment. Then, the planner searches the tree for a particular configuration, which is the nearest node to this newly generated sample. Next, a new node is created by moving a predefined distance from in the direction of the selected node using a local planner or an interpolation technique that relies on the robotic system. And, finally, if the new node is a valid point that falls in free configuration space, and if the local path between it and the nearest node is collision free, then, the new node is added to the tree as a new node and an edge is created between the tree and the new node. This process is repeated until the goal configuration can be connected to the tree or a maximum number of iterations are reached.

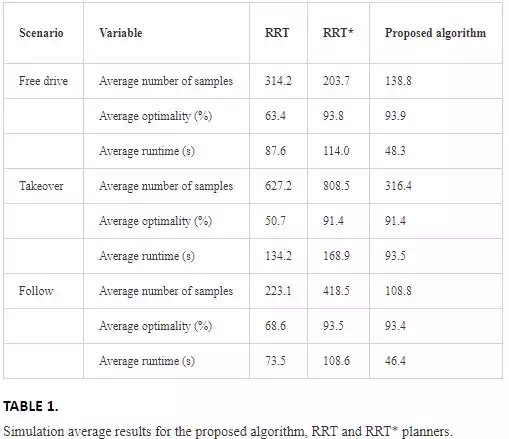
One of the key issues in sampling-based planners is that they usually result in undesirable lengthy resulted paths that stray within the free configuration space. Recently, the RRT planner has been proven not to be able to find the optimum answer. Thus, the optimal improved forms of original sampling-based algorithms, i.e. PRM* and RRT*, have been proposed and proven to possess the asymptotical optimality in which the chance of generating the optimum path approaches unity as the cardinality of the generated structure approaches infinity. The RRT* planner contains a unique ability which is the sufficiency to find the optimal path from the start position to any configuration within the free space. Figure 1 shows the performance of PRM* and RRT* algorithms in a 2D indoor environment.

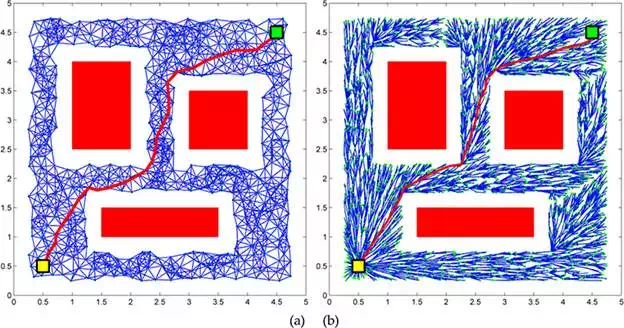
FIGURE 1.

Performances of (a) PRM* and (b) RRT* algorithms in a simple 2D environment. Start and goal configurations are shown by yellow and green squares, respectively.

Related work

Over the past two decades, sampling-based motion planning algorithms have attracted the attention of researchers in the field of autonomous vehicle resulting in various approaches with different advantages and drawbacks. In this section, some of the well-known past applications of sampling-based methods in autonomous vehicle navigation is summarized.

In one of the first reports of such applications, a probabilistic planning process has been proposed to deal with dynamic systems in dealing with static and dynamic obstacles. This planner evaluates the dynamic limitations of the vehicle’s movement and provides a steady and solid decoupling between low-level control and motion planning at the same time. This planning method maintains the convergence characteristics of its kinematic peers. The safety of the system is also considered in the form of finite running times by checking the behaviour of the planner when the existed embedded computational resources are moderate, and the motion generation process must take place in real time. This method is capable of dealing with vehicles if their dynamics are defined by ordinary differential equations or even by other hybrid complex representations.

A detailed analysis of the motion planning subsystem for the MIT DARPA Urban Challenge vehicle based on the rapidly exploring random tree (RRT) algorithm has been provided. The purpose was to present the numerous extensions made to the standard RRT algorithm that enables the online use of RRT on robotic vehicles with complex, unstable dynamics and significant drift, while preserving safety in the face of uncertainty and limited sensing.

A real-time motion planning algorithm has been introduced based on the rapidly exploring random tree (RRT) approach for autonomous vehicle operating in an urban environment. For several motivations, such as the need to generate dynamically feasible plans in real time, safety requirements and the constraints dictated by the uncertain operating (urban) environment, several extensions to the standard RRT planner have been considered.

A rapidly exploring random tree (RRT) based on path planner has been implemented for autonomous vehicle parking problem, which treats all the situations in a unified manner. As the RRT method sometimes generates some complicated paths, a smoothing sub-process has also been implemented for smoothing generated paths.

The use of rapidly exploring random trees (RRT) for the planning of multiple vehicles in traffic scenarios has been proposed. According to this method, the controller for each car uses RRT to produce a navigation plan. Spline curves are used for smoothing the route resulted from the RRT, which includes non-holonomic constraints. Priority is taken into consideration as a coordination method where a vehicle with higher priority attempts to avoid all lower priority vehicles. This algorithm attempts to find the maximum possible velocity at which the vehicle can travel and the corresponding path.

Time-efficient manoeuvres for an off-road vehicle taking tight turns with high speed on a loose surface have been studied using the RRT* planner. The experimental results have shown that the aggressive skidding manoeuvre, normally known as the trail-braking manoeuvre, naturally rises from the RRT* planner as the minimum-time path. Along the way, the RRT* planner has been extended to deal with complicated dynamical systems, such as systems that are explained by nonlinear differential equations and include high-dimensional state spaces, which may be of independent interest. The RRT* has also been exploited as an anytime computation framework for nonlinear optimization problems.

An efficient motion planning method for on-road driving of the autonomous vehicle has been reported based on the rapidly exploring random tree (RRT) algorithm]. To address the issue and taking into account the realistic context of on-road autonomous driving, they have proposed a fast RRT planner that utilizes a rule-template set according to the traffic scenes and an aggressive extension strategy for searching the tree. Both justification result in a faster and more accurate RRT planner towards the final state compared with the original RRT algorithm. Meanwhile, a model-based post-process estimation approach has been taken into account, where the resulted paths can be more smoothed and a feasible control sequence for the vehicle would be prepared. Furthermore, in the cases with moving obstacles, a combined method of the time-efficient RRT algorithm and the configuration-time space has been used to improve the quality of the resulted path and the re-planning.

A human-RRT (rapidly exploring random tree) collaborative algorithm has been presented for path planning in urban environments. The well-known RRT algorithm has been modified for efficient planning in cluttered yet structured urban environments. To engage the expert human knowledge in dynamic re-planning of autonomous vehicle, a graphical user interface has been developed that enables interaction with the automated RRT planner in real time. The interface can be used to invoke standard planning attributes such as way areas, space constrains and waypoints. In addition, the human can draw desired trajectories using the touch interface for the RRT planner to follow. Based on new information and evidence collected by human, state-dependent risk or penalty to grow paths based on an objective function can also be specified using the interface.

An online motion planner has been proposed based on the drivers’ visual behaviour-guided rapidly exploring random tree (RRT) approach that is valid for on-road driving of autonomous vehicle. The main contribution of this work is the implementation of a guidance system for drivers’ visual search behaviour in the form of the RRT navigation algorithm. RRT usually performs poorly in various planning situations such as on-road driving of autonomous vehicles because of the uncanny trajectory, wasteful sampling and low-speed exploration strategy. In order to overcome these drawbacks, they have proposed an extension of the RRT planner that utilizes a powerful supervised sampling strategy according to the drivers’ on-road behaviour in visual search and a continuous-curvature smoothing technique based on B-spline.

A sampling-based planning technique for planning manoeuvring paths for semi-autonomous vehicle has been reported where the autonomous driving system may be taking over the driver operation. They have used rapidly exploring random tree star (RRT*) and have proposed a two-stage sampling strategy and a particular cost function to adjust RRT* to semi-autonomous driving, where, besides the standard goals for autonomous driving such as collision avoidance and lane maintenance, the deviations from the estimated path planned by the driver are accounted for. They have also proposed an algorithm to remove the redundant waypoints of the path returned by RRT*, and, by applying a smoothing technique, our algorithm returns a G-squared continuous path that is suitable for semi-autonomous vehicles.

Despite the great effort that has been put to employ sampling-based methods for autonomous vehicle navigation, there are still some problems with the performance of the current methods. For instance, there is no proper method for takeover which is one of the most common behaviours in driving. Takeover is a complicated and critical task that sometimes is not avoidable and the motion planner should be able to plan takeovers while considering the safety issues. Furthermore, the running time of the planner is usually too high which makes the method less practical. Finally, the quality of the generated solutions, i.e. paths, is a critical issue. The quality of the resulted paths from sampling-based methods is normally low and finding the optimal path is usually a challenging task in randomized algorithms.

Proposed approach

In this work, a new sampling-based motion planner is introduced for autonomous vehicle navigation. The proposed method is based on the optimality concept of the RRT* algorithm and the low-dispersion concept of the LD-RRT algorithm. Furthermore, this planner utilizes a novel procedure that divides the sampling domain based on the updates received from the vehicle’s sensory system.

ALGORITHM 1.

RRT^* Planner

The first component of the proposed planner is the RRT* algorithm that can be described in Algorithm 1.

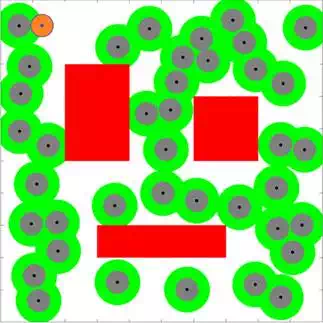
FIGURE 2.

The implementation of the boundary sampling in a simple 2D environment with three obstacles. The new sample (orange circle) will be generates on the boundary of the union of forbidden region after the occurrence of the first rejection.

In the RRT* algorithm, the important recoveries can be seen in Algorithm 1, where an edge is added to the tree only if it can be connected to the latest generated point through a set of path segments with minimal cost. Then, if other nodes exist in the vicinity of the current node with better costs, these nodes will take the position of the parent for the current node. These improvements facilitate the RRT* algorithm with the unique capability of finding the optimal solution. Figure 2 shows the optimality behaviour of the RRT* algorithm in an empty environment.

The second component of the proposed method is the low-dispersion properties of the LD-RRT planner. This component utilizes the poison disk sampling strategy to reduce the number of samples required to capture the connectivity of the sampling domain. The proposed method performance is similar to the PRM*/RRT* algorithms with a basic different in the sampling technique. Unlike the original planners that would let any collision-free samples to be included in the tree, the proposed method contains an extra checking procedure that makes sure that the samples possess the Poisson-disk distribution property.

There are various efficient techniques for creating fast Poisson-disk structures. In this research, the boundary sampling technique is selected for generating the Poisson-disk samples for its simplicity and implementation facility. In this method, the existing neighbourhood of all samples reduces to a set of spheres located at the sample’s position with the radius of r^s. The first result of such arrangement is that the existing neighbourhood can be represented by a set of spherical ranges at which a point can be placed on the boundary. Figure 3 shows the sampling phase as proposed in where the Poisson disks and the forbidden sampling areas are illustrated by grey and green circles, respectively. After the first rejection, the boundary of the union of the forbidden areas will be selected and a random sample is generated accordingly as shown by the orange circle. The sampling radius is defined as follows:

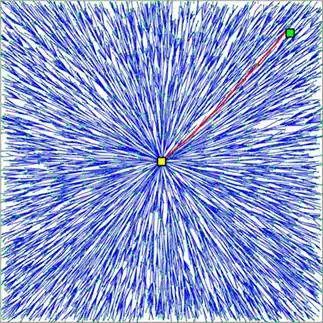
FIGURE 3.

The optimal behaviour of RRT* algorithm in a planar empty environment.

ALGORITHM 2.

The proposed asingle–uery algorithm

where τ is a scaling coefficient ranging within (0, 1]. The main idea behind this radius is that the volume of the space should be approximately equal to n(r^s)² in order to fill an obstacle-free square space with n disks with radius r^s. Compelling the samples to follow the Poisson-disk distribution usually decreases the cardinality of the resulted graph. In other words, it is almost impossible to find n samples with √τQfree/n distance from one another with a randomized sample generator. Upon the generation of the Poisson-disk samples, the algorithm will follow normal steps in the original PRM*/RRT*. The pseudo code of the proposed algorithms can be seen in Algorithm 2.

As can be seen in Algorithm 2, the Poisson-disk sampling takes place at line 4 by forcing the generated samples to satisfy the sampling radius rule. The rest of both algorithms are same as the originals. The relevance between the neighbourhood and sampling radii is an important index about the performance of the proposed algorithm. It is essential for the sampling radius to be smaller than the connection radius. Otherwise, it will not be possible to connect any two samples and the resulted structure will be a set of separate configurations. Figure 4 shows the relation between these two radii along with the ratio of r^s(n) over r*(n).

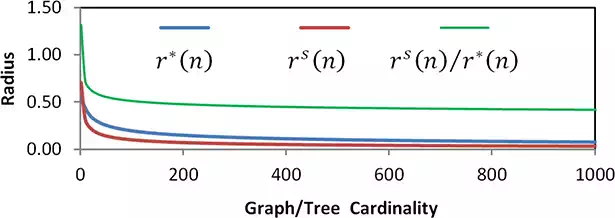
FIGURE 4.

Different values for neighbourhood and sampling radii and the corresponding ratio for μ(Q_free) = 1 and τ = 1. For n ≥ 4, the neighbourhood radius is always greater than the sampling radius.

According to the definitions of neighbourhood and sampling radii, the cardinality of the graph/tree should follow the following rule:

This requirement ensures that there will be at least one eligible sample within the neighbourhood region of the current sample. Considering the acceptable range of τ, i.e. (0, 1], the sampling radius in a 2D configuration space is smaller than the neighbourhood radius if and only if the number of samples exceeds four.

Another important property of the proposed planner takes place in the RRT* algorithm where the steering factor in the original RRT*, which is 'step', will be automatically replaced by the sampling radius. As stated before, the samples will be created randomly from the perimeter of the current Poisson disks. As a result, the highest distance between any two samples exactly equals the sampling radius r^s(n). As stated before, the cost of the final optimum solution can be calculated as the total Euclidean distance between all members (nodes) of the optimum path which can be calculated as follows:

where n* is the number of nodes in the optimal path resulted from the algorithm. Considering the fact that ∥ω∗i+1−ω∗i∥<rs(n), now it is possible to find an upper bound for the path of the optimal solution:

This upper bound merely depends on the size of the final graph/tree structure. On the other hand, reducing the total number of samples (n), will reduce the number of samples in any solution. Therefore, it can be concluded that using a Poisson-disk distribution as the sampling domain will improve the cost of the final solution and maintains the asymptotic optimality property of the proposed algorithm. Figure 5 illustrates the graph construction phase for the PRM* planner.

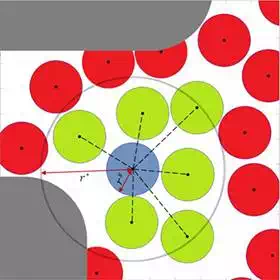
FIGURE 5.

The connection strategy in the proposed algorithm.

The next component of the proposed method is a novel procedure that divides the sampling domain into different sampling segments based on the information received online from the sensory system of the vehicle. The proposed approach divides the sampling domain into two regions namely tabu region and valid region. The sampling procedure takes place only in the valid region and the tabu region is forbidden to be included in the sampling. Figure 6 shows different possibilities of tabu and valid segments in a sampling domain.

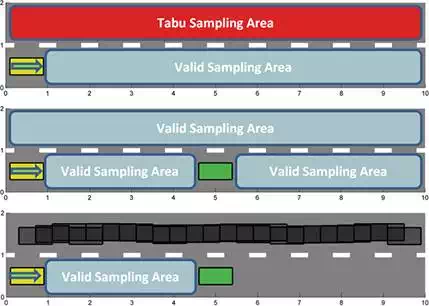
FIGURE 6.

The performance of the segmentation procedure. The sampling domain is divided into different valid or tabu segments.

Three different scenarios have been considered in the simulation studies. In the first one, there is no vehicle in front of the autonomous car and the sampling domain is only the current lane. In the second situation, there is a vehicle in front but takeover is possible and the valid sampling region is expanded to include proper space for the takeover. Finally, when takeover is not possible, the valid sampling domain is restricted to the available space between the two vehicles.

Simulation studies

According to the properties of the proposed algorithm, three different situations have been designed for simulation studies. Figure 7 depicts an instance of the solutions in these scenarios. The proposed method is able to plan difficult motions for the vehicle such as following or takeover. As can be seen in Figure 7, when there are no other vehicles, the planner restricts the sampling domain to the current lane and other parts of the road are not included in the sampling procedure. When there is another car in front but takeover is not an option, the generated rapidly exploring random tree just follows the front vehicle with a proper distance. Finally, when takeover is possible, the sampling domain will be expanded to include suitable space.

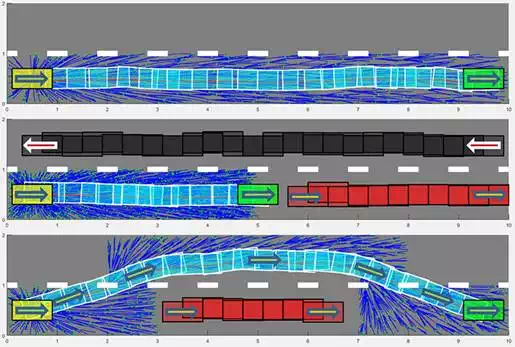
FIGURE 7.

Simulation results in different scenarios. The initial and final positions of the vehicle are shown by yellow and green, respectively.

The average results of the performance of the proposed planner as well as the performances of RRT and RRT* planners are shown in Table 1.

As can be seen, the proposed planner provides optimal solutions with surprisingly smaller set of samples. The runtime of the planner is also less than other planners. Figure 8 shows the variations of performance variables for 1000 iterations of each planner.

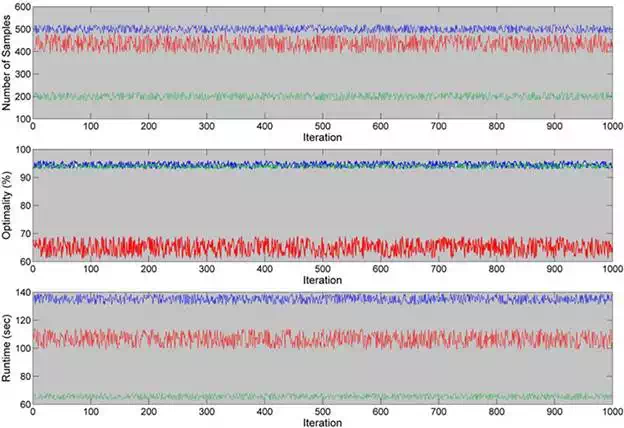
FIGURE 8.

Variation of the results over 1000 iterations for the proposed algorithm (green), RRT (red) and RRT* (blue) in terms of the number of nodes, optimality (%) and runtime (s).

Conclusion

In this chapter, a novel sampling-based navigation architecture has been introduced that is capable of driving autonomous vehicles in crowded environments. The proposed planner utilizes the optimal behaviour of the RRT* algorithm combined with the low runtime requirements of low-dispersion sampling-based motion planning. Furthermore, a novel segmentation procedure is introduced which differentiates between valid and tabu segments of the sampling domain in different situations.

Simulation results show the robust performance of this planner in different scenarios such as following the front car and takeover. This method also outperforms the classical RRT and RRT* planners in terms of runtime and the size of the generated tree while maintaining the same optimality rate as RRT*.