PID Loop Tuning Methods for Robotics

PID loop tuning is a programming method that allows a user to vary any combination of three variables to produce the desired effects within a closed system. Here we will discuss common forms of PID tuning as well as situations in which no PID is needed.

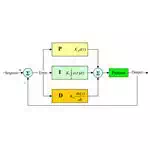
The PID, as the name itself implies has three main coefficients which affect the system response, varying these coefficients will give different results. A PID algorithm compares the system output against a calibrated or reference value. A reference value is a standardized result and based on that, system output is changed to achieve desired results. The best thing about a PID controller is that it is tunable and scalable. You do not need to vary all the three coefficients, you can change just one coefficient, or change two different coefficient by making combination or change all of them, depending upon your requirements and this is what we call loop tuning of a PID controller.

 PID and Robotics

Robotics means automated control of machines. PID controllers go hand in hand with robotics as they bring accuracy into the system. However not every robotic device will require you to put a PID controller and vary your parameters. There are certain conditions that decide if you need PID loop tuning or not.

You surely need a PID controller when your system is linear. For non-linear devices, characteristics properties and parameter values will change with change in the curve of the graph, which means at every point of the curve, you will need to change your parameter gains. If the graph is linear, you can change parameter gains as a whole.

You do not need a PID controller under the following conditions:

○  If your reference output and system output match, you get what you want, there is no need for loop tuning of PID.

○ If the system response of your system does not show any error and there is no need to improve upon its characteristics, you do not need PID.

○ If all the input parameters are working fine and the system is not showing any dangerous output characteristics.

Different Methods for Loop Tuning in Robotics

PID loop tuning given the natural frequency of the parameter gains can be manipulated using different methods. Here are some of the most popular loop tuning methods that are tested by times and trusted by people all over the world.

Ziegler Nicholas Method is arguable the most popular and reliable method for tuning a PID loop. This method includes setting the D and I gains to zero value. The parameters which are monitored and manipulated in this method are Proportional Gain (Kp ), Ultimate Period (Pu) and Oscillation Period (Tu). The P, I and D gains are now set against oscillation period and ultimate gain so that desired output is achieved.This method can be used for both the open and closed loop systems.

The basic formula used in the Ziegler Nicholas method for tuning is : Kc = 0.45Ku and Tu = (Pu/1.2)

Cohen-Coon Method is suitable only for open loop systems and it can only be used for time delay models that belong to t he first order class. It corrects the steady-state response given by the Ziegler Nicholas method. Cohen Coon method is an offline method, whereas Ziegler Nicholas method is an online method. For every tuning cycle, a steady state must be achieved because in offline methods steady state only leads towards step change in the input.The corresponding image shows parameters used in the Cohen Coon method.

Automatic Tuning based on relay feedback is another method that is an alternative to the conventional continuous cycling technique. This method is also known as Auto Tune Variation (AV) Method. It is performed for closed-loop systems and it is efficient for long time constant processes as compared to the conventional hit and trial or step methods.

Advancement in technology has made it possible to perform loop tuning and visualize the changes taking place on screen. LabView is one such tool that helps in monitoring and optimizing control systems using graphical flowcharts. Another tool is Robust Control Toolbox from Matlab. This tool minimizes overshoot and keeps a check on the steady state errors. It also offers approximation algorithms for model order reduction.