Wind Turbine Aerodynamics Design

The wind turbine aerodynamics of a horizontal-axis wind turbine (HAWT) are not straightforward. The air flow at the blades is not the same as the airflow further away from the turbine. The very nature of the way in which energy is extracted from the air also causes air to be deflected by the turbine. In addition the aerodynamics of a wind turbine at the rotor surface exhibit phenomena that are rarely seen in other aerodynamic fields.

Axial momentum and the Betz limit

$Description: C:\Users\Admin\Desktop\Size Reduced assets\Size reduced\Powerplant Engg\assets\wind_power\9_files\image002.webp$

Energy in fluid is contained in four different forms: gravitational potential energy, thermodynamic pressure, kinetic energy from the velocity and finally thermal energy. Gravitational and thermal energy have a negligible effect on the energy extraction process. From a macroscopic point of view, the air flow about the wind turbine is at atmospheric pressure. If pressure is constant then only kinetic energy is extracted. However up close near the rotor itself the air velocity is constant as it passes through the rotor plane. This is because of conservation of mass. The air that passes through the rotor cannot slow down because it needs to stay out of the way of the air behind it. So at the rotor the energy is extracted by a pressure drop. The air directly behind the wind turbine is at sub-atmospheric pressure; the air in front is under greater than atmospheric pressure. It is this high pressure in front of the wind turbine that deflects some of the upstream air around the turbine.

$Description: C:\Users\Admin\Desktop\Size Reduced assets\Size reduced\Powerplant Engg\assets\wind_power\9_files\image004.webp$

Albert Betz and Frederick W. Lanchester were the first to study this phenomenon. Betz notably determined the maximum limit to wind turbine performance. The limit is now referred to as the Betz limit. This is derived by looking at the axial momentum of the air passing through the wind turbine. As stated above some of the air is deflected away from the turbine. This causes the air passing through the rotor plane to have a smaller velocity than the free stream velocity. The ratio of this reduction to that of the air velocity far away from the wind turbine is called the axial induction factor. It is defined as below:

$Description: a\equiv\frac{U_1-U_2}{U_1}$

where: a is the axial induction factor, U1 is the wind speed far away upstream from the rotor, and U2 is the wind speed at the rotor.

The first step to deriving the Betz limit is applying conservation of axial momentum. As stated above the wind loses speed after the wind turbine compared to the speed far away from the turbine. This would violate the conservation of momentum if the wind turbine was not applying a thrust force on the flow. This thrust force manifests itself through the pressure drop across the rotor. The front operates at high pressure while the back operates at low pressure. The pressure difference from the front to back causes the thrust force. The momentum lost in the turbine is balanced by the thrust force.

Another equation is needed to relate the pressure difference to the velocity of the flow near the turbine. Here the Bernoulli equation is used between the field flow and the flow near the wind turbine. There is one limitation to the Bernoulli equation: the equation cannot be applied to fluid passing through the wind turbine. Instead conservation of mass is used to relate the incoming air to the outlet air. Betz used these equations and managed to solve the velocities of the flow in the far wake and near the wind turbine in terms of the far field flow and the axial induction factor. The velocities are given below as:

U₂ = U₁(1 − a)

U₄ = U₁(1 − 2a)

U4 is introduced here as the wind velocity in the far wake. This is important because the power extracted from the turbine is defined by the following equation. However the Betz limit is given in terms of the coefficient of power. The coefficient of power is similar to efficiency but not the same. The formula for the coefficient of power is given beneath the formula for power:

$Description: P=0.5\rho AU_2(U_1^2-U_4^2)$

$Description: C_p\equiv\frac{P}{0.5\rho AU_1^3}$

Betz was able to develop an expression for Cp in terms of the induction factors. This is done by the velocity relations being substituted into power and power is substituted into the coefficient of power definition. The relationship Betz developed is given below:

C_p = 4a(1 − a)²

The Betz limit is defined by the maximum value that can be given by the above formula. This is found by taking the derivative with respect to the axial induction factor, setting it to zero and solving for the axial induction factor. Betz was able to show that the optimum axial induction factor is one third. The optimum axial induction factor was then used to find the maximum coefficient of power. This maximum coefficient is the Betz limit. Betz was able to show that the maximum coefficient of power of a wind turbine is 16/27. Airflow operating at higher thrust will cause the axial induction factor to rise above the optimum value. Higher thrust cause more air to be deflected away from the turbine. When the axial induction factor falls below the optimum value the wind turbine is not extracting all the energy it can. This reduces pressure around the turbine and allows more air to pass through the turbine, but not enough to account for lack of energy being extracted.

The derivation of the Betz limit shows a simple analysis of wind turbine aerodynamics. In reality there is a lot more. A more rigorous analysis would include wake rotation, the effect of variable geometry. The effect of air foils on the flow is a major component of wind turbine aerodynamics. Within airfoils alone, the wind turbine aerodynamicist has to consider the effect of surface roughness, dynamic stall tip losses, solidity, among other problems.

Angular momentum and wake rotation

The wind turbine described by Betz does not actually exist. It is merely an idealized wind turbine described as an actuator disk. It's a disk in space where fluid energy is simply extracted from the air. In the Betz turbine the energy extraction manifests itself through thrust. The equivalent turbine described by Betz would be a horizontal propeller type operating with infinite blades at infinite tip speed ratios and no losses. The tip speed ratio is ratio of the speed of the tip relative to the free stream flow. This turbine is not too far from actual wind turbines. Actual turbines are rotating blades. They typically operate at high tip speed ratios. At high tip speed ratios three blades are sufficient to interact with all the air passing through the rotor plane. Actual turbines still produce considerable thrust forces.

One key difference between actual turbines and the actuator disk, is that the energy is extracted through torque. The wind imparts a torque on the wind turbine, thrust is a necessary by-product of torque. Newtonian physics dictates that for every action there is an equal and opposite reaction. If the wind imparts a torque on the blades then the blades must be imparting a torque on the wind. This torque would then cause the flow to rotate. Thus the flow in the wake has two components, axial and tangential. This tangential flow is referred to as wake rotation.

Torque is necessary for energy extraction. However wake rotation is considered a loss. Accelerating the flow in the tangential direction increases the absolute velocity. This in turn increases the amount of kinetic energy in the near wake. This rotational energy is not dissipated in any form that would allow for a greater pressure drop (Energy extraction). Thus any rotational energy in the wake is energy that is lost and unavailable.

This loss is minimized by allowing the rotor to rotate very quickly. To the observer it may seem like the rotor is not moving fast; however, it is common for the tips to be moving through the air at 6 times the speed of the free stream. Newtonian mechanics defines power as torque multiplied by the rotational speed. The same amount of power can be extracted by allowing the rotor to rotate faster and produce less torque. Less torque means that there is less wake rotation. Less wake rotation means there is more energy available to extract.

Blade Element and Momentum Theory

The simplest model for horizontal axis wind turbine (HAWT) aerodynamics is Blade Element Momentum (BEM) theory. The theory is based on the assumption that the flow at a given annulus does not affect the flow at adjacent annuli. This allows the rotor blade to be analyzed in sections, where the resulting forces are summed over all sections to get the overall forces of the rotor. The theory uses both axial and angular momentum balances to determine the flow and the resulting forces at the blade.

The momentum equations for the far field flow dictate that the thrust and torque will induce a secondary flow in the approaching wind. This in turn affects the flow geometry at the blade. The blade itself is the source of these thrust and torque forces. The force response of the blades is governed by the geometry of the flow, or better known as the angle of attack. Refer to the Airfoil article for more information on how airfoils create lift and drag forces at various angles of attack. This interplay between the far field momentum balances and the local blade forces requires one to solve the momentum equations and the airfoil equations simultaneously. Typically computers and numerical methods are employed to solve these models.

There is a lot of variation between different version of BEM theory. First, one can consider the effect of wake rotation or not. Second, one can go further and consider the pressure drop induced in wake rotation. Third, the tangential induction factors can be solved with a momentum equation, an energy balance or orthognal geometric constraint; the latter a result of Biot-Savart law in vortex methods. These all lead to different set of equations that need to be solved. 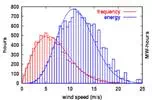The simplest and most widely used equations are those that consider wake rotation with the momentum equation but ignore the pressure drop from wake rotation. Those equations are given below. a is the axial component of the induced flow, a' is the tangential component of the induced flow. σ is the solidity of the rotor, φ is the local inflow angle. C_n and C_t are the coefficient of normal force and the coefficient of tangential force respectively. Both these coefficients are defined with the resulting lift and drag coefficients of the airfoil:

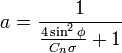
$Description: a=\frac{1}{\frac{4\sin^2\phi}{C_n\sigma}+1}$

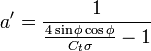
$Description: a'=\frac{1}{\frac{4\sin\phi \cos\phi}{C_t\sigma}-1}$

Corrections to Blade Element Momentum theory

Blade Element Momentum (BEM) theory alone fails to accurately represent the true physics of real wind turbines. Two major shortcomings are the effect of discrete number of blades and far field effects when the turbine is heavily loaded. Secondary short-comings come from dealing with transient effects like dynamic stall, rotational effects like coriolis and centrifugal pumping, finally geometric effects that arise from coned and yawed rotors. The current state of the art in BEM uses corrections to deal with the major shortcoming. These corrections are discussed below. There is as yet no accepted treatment for the secondary shortcomings. These areas remain a highly active area of research in wind turbine aerodynamics.

The effect of the discrete number of blades is dealt with by applying the Prandtl tip loss factor. The most common form of this factor is given below where B is the number of blades, R is the outer radius and r is the local radius. The definition of F is based on actuator disk models and not directly applicable to BEM. However the most common application multiplies induced velocity term by F in the momentum equations. As in the momentum equation there are many variations for applying F, some argue that the mass flow should be corrected in either the axial equation, or both axial and tangential equations. Others have suggested a second tip loss term to account for the reduced blade forces at the tip. Shown below are the above momentum equations with the most common application of 'F':

$Description: F=\frac{2}{\pi}\cos^{-1}(e^{-(\frac{B*(R-r)}{2r\sin\phi})})$

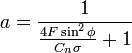
$Description: a=\frac{1}{\frac{4F\sin^2\phi}{C_n\sigma}+1}$

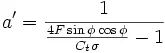
$Description: a'=\frac{1}{\frac{4F\sin\phi \cos\phi}{C_t\sigma}-1}$

The typical momentum theory applied in BEM is only effective for axial induction factors up to 0.4 (thrust coefficientof 0.96). Beyond this point the wake collapses and turbulent mixing occurs. This state is highly transient and largely unpredictable by theoretical means. Accordingly, several empirical relations have been developed. As the usual case there are several version, however a simple one that is commonly used is a linear curve fit given below, with a_c = 0.2. The turbulent wake function given excludes the tip loss function, however the tip loss is applied simply by multiplying the resulting axial induction by the tip loss function.

when a > a_c

Please note the following: do not confuse C_T and C_t, the first one is the thrust coefficient of the rotor, which is the one which should be corrected for high rotor loading (i.e. for high values of a), whilst the second one (c_t) is the tangential aerodynamic coefficient of an individual blade element, which is given by the aerodynamic lift and drag coefficients.

Other Methods of Aerodynamic Modeling

BEM is widely used due to its simplicity and overall accuracy, but its originating assumptions limit its use when the rotor disk is yawed, or when other non-axisymmetric effects (like the rotor wake) influence the flow. Limited success at improving predictive accuracy has been made using computational fluid dynamics (CFD) solvers based on Reynolds Averaged Navier Stokes (RANS) and other similar three-dimensional models such as free vortex methods. These are very computationally-intensive simulations to perform for several reasons. First, the solver must accurately model the far-field flow conditions, which can extend several rotor diameters up- and down-stream and include atmospheric boundary layer turbulence, while at the same time resolving the small-scale boundary-layer flow conditions at the blades' surface (necessary to capture blade stall). In addition, many CFD solvers have difficulty meshing parts that move and deform, such as the rotor blades. Finally, there are many dynamic flow phenomena that are not easily modelled by RANS, such as dynamic stall and tower shadow. Due to the computational complexity, it is not currently practical to use these advanced methods for wind turbine design, though research continues in these and other areas related to helicopter and wind turbine aerodynamics.

Free vortex models (FVM) and Lagrangian particle vortex methods (LPVM) are both active areas of research that seek to increase modelling accuracy by accounting for more of the three-dimensional and unsteady flow effects than either BEM or RANS. FVM is similar to lifting line theory in that it assumes that the wind turbine rotor is shedding either a continuous vortex filament from the blade tips (and often the root), or a continuous vortex sheet from the blades' trailing edges. LPVM can use a variety of methods to introduce vorticity into the wake. Biot-Savartsummation is used to determine the induced flow field of these wake vorticies' circulations, allowing for better approximations of the local flow over the rotor blades. These methods have largely confirmed much of the applicability of BEM and shed insight into the structure of wind turbine wakes. FVM has limitations due to its origin in potential flow theory, such as not explicitly modelling model viscous behavior, though LPVM is a fully viscous method. LPVM is more computationally intensive than either FVM or RANS, and FVM still relies on blade element theory for the blade forces.