SEMI-STEADY STATE SOLUTION

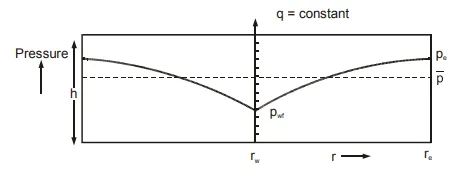
The radial diffusivity equation, (5.20), will be solved under semi-steady state flow conditions for the geometry and radial pressure distribution shown in fig.

At the time when the solution is being sought the volume averaged pressure within the cell is p which can be calculated from the following simple material balance

in which V is the pore volume of the radial cell, q is the constant production rate and t the total flowing time. The corresponding boundary pressures at the time of solution are pe at re and pwf at rw. For the drainage of a radial volume cell, the semi-steady state condition was derived in the previous chapter as

in which the van Everdingen skin factor has been included as described in Chapter 4, sec. 7. One unfortunate aspect concerning the application of this equation is that, while both q and pwf can be measured directly, the outer boundary pressure cannot. It is therefore more common to express the pressure drawdown in terms of p − pwf instead of pe − pwf, since p , the average pressure within the drainage volume, can readily be determined from a well test as will be shown in Chapter 7, sec. 7. To express the inflow equation in these terms requires the determination of the volume averaged pressure within the radial cell as