DERIVATION OF THE BASIC RADIAL DIFFERENTIAL EQUATION

The basic differential equation will be derived in radial form thus simulating the flow of fluids in the vicinity of a well. Analytical solutions of the equation can then be obtained under various boundary and initial conditions for use in the description of well testing and well inflow, which have considerable practical application in reservoir engineering. This is considered of greater importance than deriving the basic equation in cartesian coordinates since analytical solutions of the latter are seldom used in practice by field engineers.

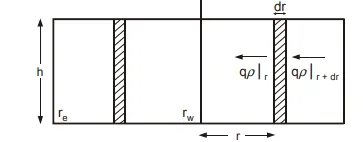
In numerical reservoir simulation, however, cartesian geometry is more commonly used but even in this case the flow into or out of a well is controlled by equations expressed in radial form such as those presented in the next four chapters. The radial cell geometry is shown in fig. 5.1 and initially the following simplifying assumptions will be made.

a) The reservoir is considered homogeneous in all rock properties and isotropic with respect to permeability.

b) The producing well is completed across the entire formation thickness thus ensuring fully radial flow.

c) The formation is completely saturated with a single fluid.

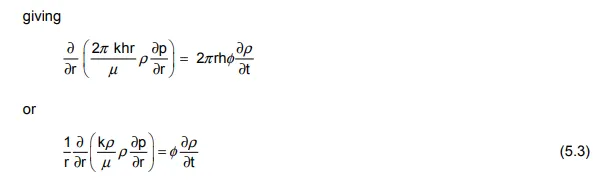
The time derivative of the density appearing on the right hand side of equ. (5.3) can be expressed in terms of a time derivative of the pressure by using the basic thermodynamic definition of isothermal compressibility.

This is the basic, partial differential equation for the radial flow of any single phase fluid in a porous medium. The equation is referred to as non-linear because of the implicit pressure dependence of the density, compressibility and viscosity appearing in the coefficients kρ /µ and φ cρ. Because of this, it is not possible to find simple analytical solutions of the equation without first linearizing it so that the coefficients somehow lose their pressure dependence. A simple form of linearization applicable to the flow of liquids of small and constant compressibility (undersaturated oil) will be considered in sec. 5.4, while a more rigorous method, using the Kirchhoff integral transformation, will be presented in Chapter 8 for the more complex case of linearization for the flow of a real gas.