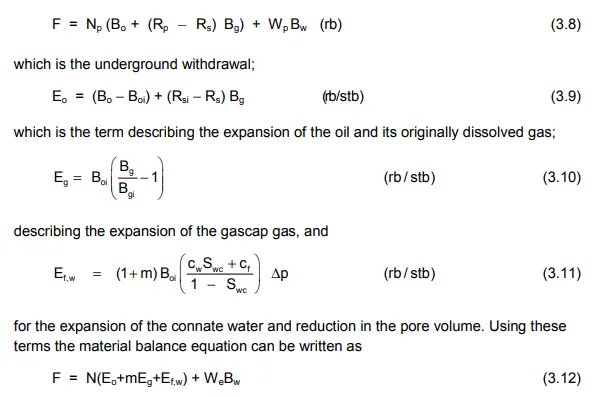
THE MATERIAL BALANCE EXPRESSED AS A LINEAR EQUATION

Since the advent of sophisticated numerical reservoir simulation techniques, the Schilthuis material balance equation has been regarded by many engineers as being of historical interest only; a technique used back in the nineteen forties and fifties when people still used slide-rules. It is therefore interesting to note that as late as 1963-4, Havlena and Odeh presented two of the most interesting papers ever published on the subject of applying the material balance equation and interpreting the results. Their papers,4,5 described the technique of interpreting the material balance as the equation of a straight line, the first paper describing the technique and the second illustrating the application to reservoir case histories.

To express equ. (3.7) in the way presented by Havlena and Odeh requires the definition of the following terms

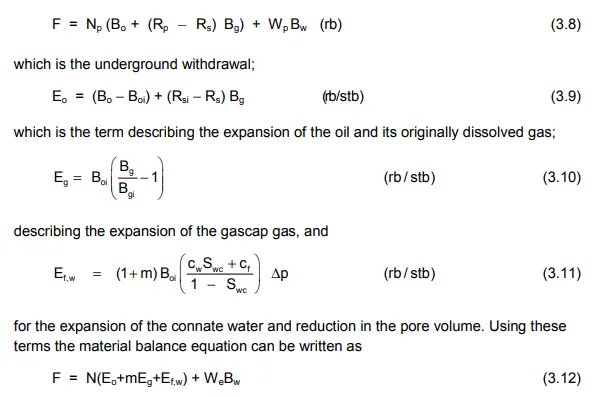
Havlena and Odeh have shown that in many cases equ. (3.12) can be interpreted as a linear function. For instance, in the case of a reservoir which has no initial gascap, negligible water influx and for which the connate water and rock compressibility term may be neglected; the equation can be reduced to

in which the observed production, evaluated as an underground withdrawal, should plot as a linear function of the expansion of the oil plus its originally dissolved gas, the latter being calculated from a knowledge of the PVT parameters at the current reservoir pressure. This interpretation technique is useful, in that, if a simple linear relationship such as equ. (3.13) is expected for a reservoir and yet the actual plot turns out to be non-linear, then this deviation can itself be diagnostic in determining the actual drive mechanisms in the reservoir. For instance, equ. (3.13) may turn out to be non-linear because there is an unsuspected water influx into the reservoir helping to maintain the pressure. In this case equ. (3.12) can still be expressed in a linear form as

Once a straight line has been achieved, based on matching observed production and pressure data, then the engineer has, in effect, built a suitable mathematical model to describe the performance of the reservoir. As previously described, in Chapter 1, sec. 7, this phase is commonly referred to as a history match. Once this has been satisfactorily achieved, the next step is to use the same mathematical model to predict how the reservoir will perform in the future, possibly for a variety of production schemes. This prediction phase is facilitated by the mathematical ease in using the simple linear expressions for the material balance equation, as presented by Havlena and Odeh. The technique will be illustrated in greater detail in the following sections.