GENERAL FORM OF THE MATERIAL BALANCE EQUATION FOR A HYDROCARBON RESERVOIR

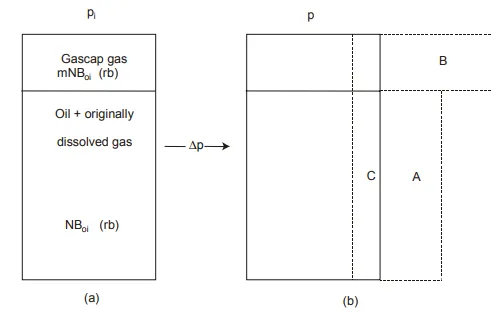
The general form of the material balance equation was first presented by Schilthuis1 in 1941. The equation is derived as a volume balance which equates the cumulative observed production, expressed as an underground withdrawal, to the expansion of the fluids in the reservoir resulting from a finite pressure drop. The situation is depicted in fig. 3.1 in which (a) represents the fluid volume at the initial pressure pi in a reservoir which has a finite gascap. The total fluid volume in this diagram is the hydrocarbon pore volume of the reservoir (HCPV). Fig. 3.1 (b) illustrates the effect of reducing the pressure by an amount ∆p and allowing the fluid volumes to expand, in an artificial sense, in the reservoir. The original HCPV is still drawn in this diagram as the solid line. Volume A is the increase due to the expansion of the oil plus originally dissolved gas, while volume increase B is due to the expansion of the initial gascap gas. The third volume increment C is the decrease in HCPV due to the combined effects of the expansion of the connate water and reduction in reservoir pore volume as already discussed in Chapter 1, sec. 7. If the total observed surface production of oil and gas is expressed in terms of an underground withdrawal, evaluated at the lower pressure p, (which means effectively,

taking all the surface production back down to the reservoir at this lower pressure) then it should fit into the volume A + B + C which is the total volume change of the original HCPV. Conversely, volume A + B + C results from expansions which are allowed to artificially occur in the reservoir. In reality, of course, these volume changes correspond to reservoir fluid which would be expelled from the reservoir as production. Thus the volume balance can be evaluated in reservoir barrels as