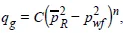....................(1)Gas well deliverability
Early estimates of gas well performance were conducted by opening the well to the atmosphere and then measuring the flow rate. Such “open flow” practices were wasteful of gas, sometimes dangerous to personnel and equipment, and possibly damaging to the reservoir. They also provided limited information to estimate productive capacity under varying flow conditions. The idea, however, did leave the industry with the concept of absolute open flow (AOF). AOF is a common indicator of well productivity and refers to the maximum rate at which a well could flow against a theoretical atmospheric backpressure at the reservoir.
The productivity of a gas well is determined with deliverability testing. Deliverability tests provide information that is used to develop reservoir rate-pressure behavior for the well and generate an inflow performance curve or gas-backpressure curve.
Analyzing deliverability test data
There are two basic relations currently in use to analyze deliverability test data. An empirical relationship was proposed by Rawlins and Schellhardt in 1935 and is still frequently used today. Houpeurt presented a theoretical deliverability relationship derived from the generalized radial diffusivity equation accounting for non-Darcy flow effects.
Rawlins and Schellhardt developed the empirical backpressure method of testing gas wells based on the analysis of tests on more than 500 wells. They noted that when the difference between the squares of the average reservoir pressure and flowing bottomhole pressures were plotted against the corresponding flow rates on logarithmic coordinates, they obtained a straight line. This led them to propose the backpressure equation:
....................(1)
where C is the flow coefficient and n is the deliverability exponent. The deliverability exponent is the inverse of the slope of the curve. Once n is determined, C can be obtained by substituting pressure and rate data read directly from the straight-line plot into Eq. 1 and solving the resulting relation.
As discussed previously, solutions for gas well performance in terms of pressure-squared are appropriate only at low reservoir pressures. As a result, Rawlins and Schellhardt’s deliverability equation can be rewritten in terms of pseudopressure as
....................(2)
where C and n are determined in the same manner as for Eq. 1. The values of n range from 0.5 to 1.0, depending on flow characteristics. Flow characterized by Darcy’s equation will have a flow exponent of 1.0, while flow that exhibits non-Darcy flow behavior will have a flow exponent ranging from 0.5 to 1.0. While the Rawlins and Schellhardt deliverability equation is not rigorous, it is still widely used in deliverability analysis and has provided reasonable results for high-permeability gas wells over the years.
Eqs. 1 and 2 can be rewritten to facilitate the development of the inflow performance curve. In terms of pressure-squared, the relationship is
....................(3)
and 
....................(4)
in terms of pseudopressure. Once the deliverability exponent is determined from a multirate test and the AOF estimated, Eqs. 3 and 4 can be applied readily to estimate the rate for a given flowing bottomhole pressure.
Houpeurt developed a theoretical deliverability relationship for stabilized flow with a Forchheimer[3] velocity term to account for non-Darcy flow effects in high-velocity gas production. The resulting relationship can be written in terms of pressure-squared or pseudopressure as
....................(5)
or 
....................(6)
Eqs. 5 and 6 are quadratic in terms of the flow rate, and the solutions can be written for convenience as shown in Eqs. 7 and 8.
....................(7)
....................(8)
Jones, Blount, and Glaze[4] suggested Houpeurt’s relationship be rewritten as shown in Eqs. 9 and 10 to allow the analysis of well-test data to predict deliverability.
....................(9)
....................(10)
A plot of the difference in pressures squared divided by the flow rate or the difference in pseudopressure divided by the flow rate vs. the flow rate yields a straight line on a coordinate graph. The intercept of the plot is the laminar flow coefficient a, while turbulence coefficient b is obtained from the slope of the curve. Once these two coefficients have been determined, deliverability can be estimated from the following relationships in terms of pressure-squared or pseudopressure.
....................(11)
and 
....................(12)
After the coefficients of the deliverability equations have been determined, the relationships can be used to estimate production rates for various bottomhole flowing pressures. This determination of rate vs. pressure is often referred to as the reservoir inflow performance, which is a measure of the ability of the reservoir to produce gas to the wellbore. The inflow performance curve is a plot of bottomhole pressure vs. production rate for a particular well determined from the gas well deliverability equations. Fig. 1 depicts a typical gas well inflow performance curve. This curve allows one to estimate the production rate for different flowing bottomhole pressures readily.
Fig. 1—Typical gas well inflow performance curve.
Deliverability test methods
Several different deliverability test methods have been developed to collect the data for use with the basic deliverability models. These tests can be grouped into three basic categories:
· Tests that use all stabilized data
· Tests that use a combination of stabilized and transient data
· Tests that use all transient data
The basic deliverability test method that uses all stabilized data is the flow-after-flow test. Deliverability test methods that use both transient and stabilized test data include the isochronal and modified isochronal tests. The multiple modified isochronal test consists of all transient test data and eliminates the need for stabilized flow or pressure data.
Flow-after-flow tests
Rawlins and Schellhardt1 presented the basic deliverability test method that uses all stabilized data. The test consists of a series of flow rates. The test is often referred to as a four-point test, because many tests are composed of four rates, as required by various regulatory bodies. This test is performed by producing the well at a series of stabilized flow rates and obtaining the corresponding stabilized flowing bottomhole pressures. In addition, a stabilized shut-in bottomhole pressure is required for the analysis. A major limitation of this test method is the length of time required to obtain stabilized data for low-permeability gas reservoirs.