Capillary Pressure

Curvature at an interface between wetting and nonwetting phases causes a pressure difference that is called capillary pressure. This pressure can be viewed as a force per unit area that results from the interaction of surface forces and the geometry of the system. Based on early work in the nineteenth century of Laplace, Young, and Plateau (e.g., Reference 94), a general expression for capillary pressure, Pc, as a function of interfacial tension, 0, and curvature of the interface is [19]:

where r, and rn are the principal radii of curvature at the interface. These radii are not usually measured, and a mean radius of curvature is given by the capillary pressure and interfacial tension. For a cylindrical vertical capillary, such as a small tube, the capillary pressure for a spherical interface is [19]:

where r is the radius of the tube, 6, is the contact angle measured through the more dense phase that exists between the fluid and the wall of the tube, g is the gravitational constant, p is density, h is column height, and the subscripts refer to the fluids of interest. For a fluid that wets the wall of a capillary tube, the attraction between the fluid and the wall causes the fluid to rise in the tube. The extent of rise in the capillary is proportional to the interfacial tension between the fluids and the cosine of the contact angle and is inversely proportional to the tube radius. An analogous situation can occur during two-phase flow in a porous medium. For example if capillary forces dominate in a water-wet rock, the existing pressure differential causes flow of the wetting f hid to occur through the smaller capillaries. However, if viscous forces dominate, flow will occur through the larger capillaries (from Pouiselle’s law, as a function of the 4th power of the radius). Figure 5-46 depicts a typical capillary pressure curve for a core sample in which water is the wetting phase. Variation of capillary pressure is plotted as a function of water saturation. Initially, the core is saturated with the wetting phase (water), The nonwetting phase, oil in this case, is used to displace the

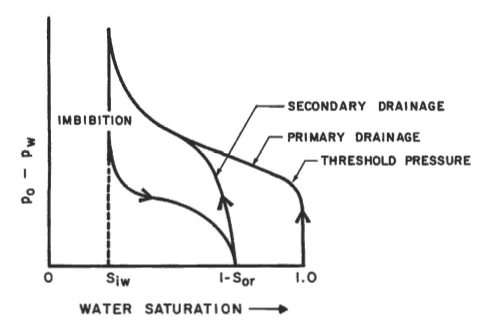
water. As shown in the figure, a threshold pressure must be overcome before any oil enters the core. The initial (or primary) drainage curve represents the displacement of the wetting phase from 100% saturation to a condition where further increase in capillary pressure causes little or no change in water saturation. This condition is commonly termed the irreducible saturation, S,. The imbibition curve reflects the displacement of the nonwetting phase (oil) from the irreducible water saturation to the residual oil saturation. Secondary drainage is the displacement of the wetting phase from the residual oil saturation to the irreducible water saturation. A hysteresis is always noted between the drainage and imbibition curves. Curves can be obtained within the hysteresis loop by reversing the direction of pressure change at some intermediate point along either the imbibition or secondary drainage curve. The nonuniform crosssection of the pores is the basic cause of the hysteresis in capillary pressure observed in porous media. Therefore, capillary pressure depends on pore geometry, interfacial tension between the fluids, wettability of the system (which will be discussed later in this chapter), and the saturation history in the medium.