Density logging

Density logging is another application of gamma rays in gathering data about subsurface formations. Density logging tools rely on gamma-gamma scattering or on photoelectric (PE) absorption.

Density logging tools

A density-logging tool sends gamma rays into a formation and detects those that are scattered back. Typical logging sondes use a Cesium-137 source, which emits gamma rays of 0.66MeV. At this high energy level, Compton scattering dominates. The average electron density in the volume of formation probed by the tool controls the scattered gamma ray count rates at the detectors. As we saw above, average electron density, in turn, correlates strongly (but not perfectly) with bulk density. Because the gamma rays cannot penetrate far into the formation, the volume of investigation is small. Mudcake and tool standoff have particularly strong effects on this measurement. For less energetic gamma rays, photoelectric (PE) absorption controls the observed count rates. Here, the average atomic number (which correlates with rock type) sets the amount of PE absorption that a formation exhibits. Again, all the bulk average effects accrue, with special problems posed by barium-weighted mud.

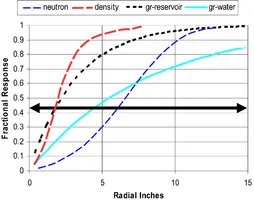
The depth of investigation of a density tool decreases with increasing density and never exceeds 6 in., as the pseudogeometric factor in Fig. 1 shows. The log almost always measures the invaded zone, at least in porous, permeable formations. As is typical of the nuclear scattering family of measurements, the density tool uses two detectors at progressively longer distances from the source. The distance between the near and far detectors sets the vertical resolution, approximately 10 in. typically. Correction is by the spine-and-ribs technique. The spine is the normal calibrated relationship between the density measured by the near-spaced and far-spaced detectors in the absence of any gap between the tool and the borehole wall. Gaps cause departures from this spine and lead to density corrections that are applied to the density from the long-space detector. This correction is presented as a curve with the density log. Above an inch or so of standoff, the compensation fails. There is no universal correction threshold, but corrections greater than 0.05 to 0.1 g/cm3 are suspicious. Unfortunately, a low correction does not guarantee a good measurement. Connecting a particular rib back to the correct location on the spine (and, hence, to the correct bulk density) requires that the density pad be parallel to the borehole wall. Likewise, very small water-filled gaps can give rise to large corrections that are perfectly correct.

Fig. 1 – Nuclear radial geometric functions: comparison of radial geometric functions for various nuclear logs in a 20-p.u. limestone.

Density-porosity log interpretation

In the standard sequential interpretation process, the analyst determines porosity directly from the density log. It is conceptually the easiest of the porosity logs to interpret because, if ever a tool obeyed a linear bulk mixing law, it is the density logs.

In a simple clean reservoir, the interpretation model is:

....................(1)

Solved for porosity, this yields

....................(2)

This porosity is subscripted with a T for total porosity because it draws no distinction between pore fluid and fluid possibly bound in shales. As mentioned in the general interpretation discussion, the density log rarely sees past the invaded zone, so ρfl = ρmf, the mud-filtrate density. Even if shale is present, the interpretation merely requires an additional term:

....................(3)

and the corresponding shale correction to turn total porosity into effective porosity is straightforward. Again, more sophisticated formation descriptions require more parameters, which in turn require more measured data for calibration.

In known lithology, the grain density, ρma, can be chosen from a table like Table 1. Sensitivity can be analyzed directly by taking the partial derivative of the response equation with respect to grain density. For a 30-p.u., water-filled sandstone, an error of 0.05 g/cm3 in the supposed grain density will only alter the calculated porosity by 2 p.u. A similar analysis of the sensitivity to fluid density shows that a variation of more than 0.1 g/cm 3 in the fluid density corresponds to a similar 2-p.u. error in the calculated porosity.

This is fortunate because fluid density within the density tool’s volume of investigation may be very difficult to estimate. As already discussed, because of its shallow depth of investigation, the density log is commonly a flushed-zone device, and the fluid density that it sees may be taken to be that of the mud filtrate. The effect of a small amount of immovable hydrocarbon or connate water can, more often than not, be ignored. If gas is present, its low density will produce an apparent increase in porosity. Here, we could have a case in which, to calculate density porosity, we must first know the average flushed-zone fluid saturation.

As discussed in the section about radiation transport, the biggest hitch in gamma-gamma scattering density evaluation is the difference between bulk density and electron density. The device measures electron density. As Table 1 shows, this matters only for fluids. Knowing that the tool will be used in fluid-filled rocks, the service companies transform the electron density to a water-filled, porous limestone, calibrated bulk density. The apparent density as read by the tool is thus altered to read:

....................(4)

In the principal lithologies of interest, this transformed density departs less than 0.004 g/cm3 from the true bulk density. The case of a high-porosity reservoir filled with gas (and with minimal invasion) may require additional correction beginning with the removal of this "calibration." In those cases, the analyst should use the apparent density rather than the true bulk density in any mixing-law equation.

Photoelectric (PE) absorption

In addition to gamma ray scattering, modern density tools also analyze the low-energy region of the scattered gamma ray spectrum separately. These low-energy gamma rays are subject to photoelectric absorption, which is controlled by the atomic number, Z. Z, in turn, strongly correlates with lithology (see Fig. 2). The length of the lines represents a variation from 0 (top) to 40 p.u. Note how effectively the lithologies are discriminated independent of porosity.

Fig. 2 - Z and, hence, the PEF measurement, discriminates lithologies, largely independent of porosity. The line lengths represent ranges of porosity from 0 to 40% in the respective lithologies. (There are three vertical lines corresponding to the porosity, ranging from 0 p.u. at the top to 40 p.u. at the bottom for each of the three common reservoir matrix lithologies. This illustrates that Z and, hence, PE is nearly porosity independent while strongly discriminating lithology. The x-axis takes on only three discrete values for each of the three lithologies).

The PE absorption cross section, in barns (10–24 cm2), is strongly dependent on the energy of the gamma rays, E, as well as the average atomic number, Z.

....................(5)

This means that low-energy gamma ray flux is attenuated according to

....................(6)

To suppress this energy dependence, the PE log is scaled as a PE index or factor:

....................(7)

So, in terms of Pe, the attenuation (which is what the tool actually measures) of low-energy gamma rays is simply

....................(8)

where ne is the electron-number density.

Density-weighted photoelectric factor

Unfortunately, Pe does not obey a linear, volumetric mixing law on which log analysis thrives. To get around this, a new parameter, U, was developed to represent density-weighted photoelectric factor.

....................(9)

where ρb is the formation density in g/cm3. In terms of multiple components,

....................(10)

which is a linear bulk mixing equation. Table 1 shows typical values of PEF and U for some common formation constituents.

Table 1

Nomenclature