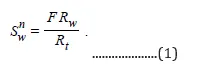
Well log interpretation

Well logs provide insight into the formations and conditions in the subsurface, aimed primarily at detection and evaluation of possibly productive horizons.

Determination of saturation

Water saturation is the fraction of the pore volume of the reservoir rock that is filled with water. It is generally assumed, unless otherwise known, that the pore volume not filled with water is filled with hydrocarbons. Determining water and hydrocarbon saturation is one of the basic objectives of well logging.

Clean formations

All water saturation determinations from resistivity logs in clean (nonshaly) formations with homogeneous intergranular porosity are based on Archie’s water saturation equation, or variations thereof.^[1][2] The equation is

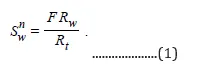
R_w is the formation water resistivity, R_t is the true formation resistivity, and F is the formation resistivity factor. F is usually obtained from the measured porosity of the formation through the relationship

where R_mf is the mud filtrate resistivity and R_xo is the flushed zone resistivity.

For simplicity, the saturation exponent n is usually taken as 2. Laboratory experiments have shown that this is a reasonable value for average cases. For more exacting work, electrical measurements on cores will produce better numbers for n, a, and m. When core measured values are unavailable, the values of a and m in Eq. 4 can be estimated as follows: in carbonates, F=1/ϕ² is usually used; in sands, F=0.62/ϕ^2[3] (Humble formula), or F=0.81/ϕ² (a simpler form practically equivalent to the Humble formula). These equations are easily programmed into spreadsheets and are available in most log interpretation software.

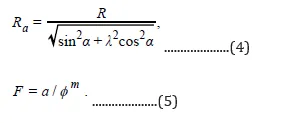
The accuracy of the Archie equation, Eq. 1 and its derivatives, depends in large measure, of course, on the accuracy of the fundamental input parameters: R_w, F, and R_t. The deep resistivity measurement (induction or laterolog) must be corrected, therefore, for borehole, bed thickness, and invasion (see the page Formation resistivity determination for more details). It is almost never safe to make the assumption "deep = R_t." The most appropriate porosity log (sonic, neutron, density, magnetic resonance, or other) or combination of porosity and lithology measurements must be used to obtain porosity, and the proper porosity-to-formation factor relationship must be used. Finally, the R_w value should be verified in as many ways as possible: calculation from the SP curve, water catalog, calculation from nearby water-bearing formation, and/or water sample measurement.

Alternate methods for determining water saturation include analysis of cores cut with low-invasion oil-based muds (OBMs) and single well chemical tracer (SWCT) tests. These independent methods can be used to calibrate log analyses.

Resistivity vs. porosity crossplots

Combining Eqs. 1 and 5, the Archie saturation equation may be written

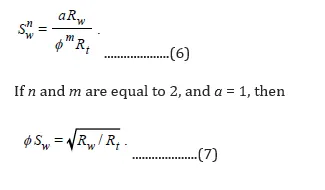
Eq. 7 shows that for R_w constant, ϕS_w is proportional to 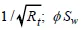 is the quantity of water per unit volume of formation. To emphasize the proportionality between ϕ and 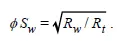, Eq. 7 may be rewritten:

Furthermore, the points corresponding to any other constant value of S_w will also fall on a straight line, because in Eq. 7 the coefficient is constant for constant values of R_w and S_w.

Fig. 1 shows several points plotted over an interval in which formation-water resistivity is constant (as indicated by constant SP deflections opposite the thick, clean permeable beds). Assuming that at least some of the points are from 100% water-bearing formations, the line for S_w = 1 is drawn from the pivot point (ϕ = 0, R_t = ∞) through the most northwesterly plotted points. The slope of this line defines the value of R_w as shown on Fig. 1, for ϕ = 10%, R₀ = 6.5 ohm•m. For this formation, the most appropriate F – ϕ relation is F = 1/ϕ². Thus, for ϕ = 10%, F = 100. Because R_w = R₀/F, R_w = 0.065 ohm•m, as shown.

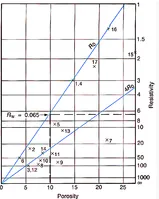
Fig. 1 – Resistivity-porosity crossplot for determining R_w and S_w.

For other S_w values, R_t and R₀ are related by the equation R_t = R₀/S_w². For S_w = 50%, and 1/S_w²=4 , and R_t = 4 R₀. This relation establishes the line for S_w = 50%. Other S_w lines may be defined in a similar manner.

If the matrix composition remains constant over the formations under investigation, the basic measurement from the sonic, density, or neutron logs can be plotted directly vs. R_t with similar results.^[4] This is possible because of the linear relationship between porosity and bulk density, sonic transit time, or neutron-hydrogen index response. An example of a sonic-induction crossplot is shown in Fig. 2. The transit time has been plotted against the induction resistivity for several levels. The northwesterly points define the 100% water saturation line. The transit-time value at the point where this line intersects the horizontal line of infinite resistivity is the matrix-transit time, t_ma In Fig. 2, t_ma is found to be approximately 47.5 μs/ft (156 μs/m). This corresponds to a matrix velocity of 21,000 ft/sec (6,400 m/s).

·        

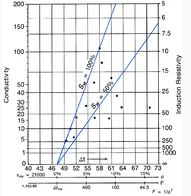
Fig. 2 – Acoustic-induction crossplot.

By knowing t_ma, a porosity scale, a scale of formation factor (e.g., from F = 1/ϕ²) can be easily derived. A vertical line drawn through F = 100 (or ϕ = 10) intersects the water line at R₀ = 5 ohm•m; accordingly, R_w (= R₀/F) is 0.05 ohm•m.

The lines for other S_w values are straight lines, determined as previously described, radiating out from the R_t =∞, t_ma = 47.5 pivot point.

Density and neutron logs can be crossplotted against resistivity in a manner identical to the sonic logs. For density logs, the intersection of the 100% water line with the infinite-resistivity line yields the matrix-density value, ρ_ma. For neutron logs, the intersection defines the matrix-hydrogen index, or apparent matrix porosity. Knowledge of matrix density or hydrogen index permits the ρ_B or ϕ_N scale to be rescaled in ϕ and F units. With the F scale defined, R_w can be calculated as for the sonic-resistivity crossplot, and lines of constant water saturation can be constructed in a similar manner.

These resistivity-vs.-porosity crossplots require that formation water resistivity be constant over the interval plotted, that lithology be constant, that invasion not be deep, and that the measured-porosity log parameter (i.e., t, ρ_B, or ϕ_N) can be linearly related to porosity. This last condition implies that the time-average transform for the conversion of t into porosity is appropriate.

The neutron-resistivity crossplot is not as satisfactory in gas-bearing formations as are the sonic- or density-resistivity crossplots. The apparent porosity measured by the neutron log in gas zones is often much too low. This results in overstated S_w values in gas zones. Indeed, in a gas zone, the neutron resistivity may indicate a porous gas-bearing zone to be near zero porosity and 100% water bearing. In contrast, the sonic- or density-resistivity tends to be slightly optimistic in gas zones (i.e., porosities may be slightly high and water saturations slightly low).

Microresistivity vs. porosity crossplots

This method is particularly useful for older logs or cases in which the analyst has only a paper copy of the log. A resistivity-porosity plot can also be made using the values from a shallow-investigation resistivity log such as the microlaterolog, MSFL, or MCFL log. If the microresistivity log reads approximately R_xo, then a line through points of mud-filtrate-saturated formations (S_xo = 1) should have a slope related to R_mf. R_mf is an important parameter, and this check of its value by means of a sonic-microresistivity or density-microresistivity crossplot is often useful.

These plots are also valuable for improved determinations of matrix parameters (either t_ma or ρ_ma), particularly in cases where the sonic-resistivity or density-resistivity plot does not give a clear answer because of hydrocarbon saturation. The F R_mf line should be easier to determine because S_xo is usually fairly high even in hydrocarbon-bearing formations.

Fig. 3 shows a resistivity-porosity plot in which both the deep induction reading and the microlaterolog at the same levels are plotted in a series of water-bearing formations. The porosity values were derived in this case from a neutron-density crossplot. The plots from the two logs define two trends corresponding respectively to S_w = 1 (using deep induction) and S_xo = 1 (using microlaterolog data). The points not in these trends can be divided into two groups:

1.     Points whose microlaterolog readings fall on the S_xo = 1 line but whose deep induction log readings fall below the S_w = 1 line (Points 2, 9, and 10) are probably the result of either deep invasion or adjacent-bed effect in which deep resistivity is greater than R_t.

2.     Points whose induction log readings fall on the S_w = 1 line but whose microlaterolog points fall above the S_xo = 1 line are possibly a result of shallow invasion in which RMLL is lower than R_xo.

Resistivity-porosity plots are thus often more informative if the short-spaced resistivity or medium-induction values are also plotted. Not only does this permit an appreciation of invasion effects, but it may also indicate moved oil.

·        

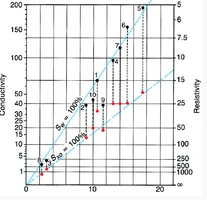
Fig. 3 – Resistivity-porosity crossplot showing points from deep-induction and microlaterolog. S_w = 1 and S_xo = 1 lines are shown.

Rwa comparison

If water saturation is assumed to be 100%, the Archie water saturation equation (Eq. 1) reduces to

....................(9)

The term R_wa is used in Eq. 9 rather than R_w to indicate that this is an apparent formation water resistivity. It is only equal to R_w in 100% water-bearing formations. In hydrocarbon-bearing formations, R_wa computed from Eq. 3 will be greater than R_w. Indeed, by combining Eqs. 10 and 5, the relationship between S_w, R_wa, and, R_w can be shown to be

....................(10)

The R_wa technique can, therefore, be useful for identifying potential hydrocarbon-bearing zones and for obtaining R_w values.

In practice, R_wa is obtained by simply dividing the deep induction resistivity (or deep laterolog resistivity) by the formation factor obtained from a porosity log or a combination of porosity logs. Today, a continuous R_wa computation is made over a long interval of the borehole in real time. If one has only paper logs, many individual manual computations are made so as to approximate a continuous computation.

Resistivity-ratio methods

In resistivity-ratio methods, it is assumed that a formation is divided into two distinct regions—a flushed zone and a noninvaded zone. Both zones have the same F, but each contains water of a distinct resistivity (R_mf in the invaded zone and R_w in the noninvaded zone). The resistivities of the two zones must be measurable or derivable from logs, and methods for determining the resistivity of the water in each zone must be available.

Because of the necessary assumptions, the resistivity-ratio methods have limitations, but when no porosity or formation factor data are available, they are sometimes the only choice. The principal limitation arises from the inability of any resistivity device to measure either R_x or R, totally independent of the other. Simply put, invasion must be deep enough to allow a shallow investigating resistivity device to measure R_xo but not so deep that a deep-resistivity device cannot measure R_t.

Another difficulty appears when hydrocarbons are present. In this case, some knowledge or assumption of the value of the flushed or invaded zone saturation is necessary.

Flushed-zone method

If n = 2 is assumed and Eq. 1 is divided by Eq. 3,

....................(11)

This equation gives the ratio of S_w to S_xo, and no knowledge of formation factor or porosity is needed. R_xo may be found from a microresistivity log, R_t from an induction or laterolog, and R_mf/R_w from measured values or from the SP curve.

The ratio is valuable in itself as an index of oil movability. If S_w/S_xo = 1, then no hydrocarbons have been moved by invasion, whether or not the formation contains hydrocarbons. If S_w/S_xo is approximately 0.7 or less, movable hydrocarbons are indicated. The value of S_w/S_xo, along with ϕ and S_wo, is useful in evaluating reservoirs.

To determine S_w from Eq. 12, S_xo must be known. For moderate invasion and average residual oil saturation, an empirical relation between S_w and S_xo has been found useful: S_xo = S_w^1/5. Inserting this into Eq. 11 gives:

....................(12)

Service companies provide charts for graphical solution of this equation, or it can be easily programmed into a spreadsheet.

Invaded-zone method

The invaded-zone method is useful for water saturation determination when only an ES, IES, or other early-resistivity log is available and no porosity-log or formation-factor data exist. (This section also uses some early nomenclature.) For application of the method, R_i/R_m must be at least 10.

Archie’s equation for the invaded zone is

....................(13)

where R_z is the resistivity of the water in the invaded zone. Because of incomplete flushing, R_z is a mixture of mud filtrate, R_mf, and formation water, R_w.

Studies of many logs suggest that S_i and S_w are related by

....................(14)

Dividing the noninvaded-zone water saturation equation (Eq. 1) by Eq. 13 and using the relationship presented in Eq. 14 yields an expression for S_w:

....................(15)

To use Eq. 15, R_t is taken from a deep resistivity device such as a deep induction or deep laterolog (corrected for borehole effect and bed thickness). R_i is taken from a shallow resistivity device such as a Laterolog 8, 16-in. normal, or SFL (corrected for borehole effect and bed thickness).

R_z is given by the relationship

....................(16)

where z is the fraction of the invaded zone pore water, which is formation water, and 1 – z is the fraction that is mud filtrate. Experience has indicated that z varies from 0.075 in cases of normal invasion to 0.035 in cases of deep invasion or vuggy formations.

Fig. 4 solves Eq. 15. It is entered with R_mf/R_w on the appropriate z scale and R_i/R_t (oblique lines) to determine S_w. When R_i/R_t is close to unity, some caution is required. The formation may be extremely invaded or there may be little invasion, or it may be dense and impermeable. On the other hand, many good hydrocarbon-bearing reservoirs will have R_i/R_t ≈ 1.

·        

Fig. 4 – Empirical resistivity-ratio method.

Rxo/Rt quicklook

The R_xo/R_t quicklook method can be used to identify hydrocarbon-bearing formations and to indicate hydrocarbon movability (producibility). When S_w/S_xo is 1 in a permeable zone, the zone will produce water or be nonproductive regardless of water saturation. A value S_w/S_xo significantly less than 1 indicates that the zone is permeable and contains some hydrocarbons, and that the hydrocarbons have been flushed (moved) by invasion. Thus, the zone contains producible hydrocarbon.

Eq. 11 can be written as

....................(17)

which shows that an indication of S_w/S_xo can be obtained by comparing R_xo/R_t with R_mf/R_w, where the subscript SP emphasizes that R_mf/R_w is derivable from the SP. Equivalently, the comparison can be between log R_xo/R_t and the SP curve for an indication of log S_w/S_xo.

The value of log R_xo/R_t is computed from solving the three or more resistivity logs for invasion parameters. It is used as an overlay comparison curve with the SP. Separations between the log R_xo/R_t curve, properly scaled to match the SP, and the SP curve provide a quick-look location of producible hydrocarbons.

Originally, log R_xo/R_t was computed from R_LL8/R_ID or R_SFL/R_ID. Use was made of the observation that over a wide range of invasion diameters (from approximately 20 to 100 in.), R_xo/R_t depends primarily on the value of R_LL8/R_ID or R_SFL/R_ID. The relationship used for the LL8 device was

....................(18)

For the SFL device, it was

....................(19)

Much more sophisticated algorithms are now used to obtain R_xo/R_t. These values are output in real time as separate logs.

To interpret the R_xo/R_t quick-look curve, the impermeable zones must be eliminated by reference to the SP, GR, or microlog curves or by resistivity ratios. Then, if the SP and R_xo/R_t (actually –K log R_xo/R_t) curves coincide in a permeable zone, the zone will most probably produce water. If, however, the R_xo/R_t curve reads appreciably lower (i.e., to the right) than the SP, the zone should produce hydrocarbons. An R_xo/R_t value less than the SP amplitude indicates movable hydrocarbons are present.

The R_xo/R_t quick-look technique is applicable to fresh mud conditions (R_xo > R_t) in formations where invasion falls within the limits demanded by the R_xo/R_t computation. For the simpler computation technique using Eq. 18 and –25, that is for d_i 30 to 70 in.; for the more sophisticated techniques, that is, between 20 and 120 in. Even in the more restrictive case, however, any errors are optimistic. In other words, water zones may appear to be hydrocarbon-productive. This constitutes a safeguard against overlooking pay zones, and it is considered a desirable feature in any quick-look approach.

The R_xo/R_t technique efficiently handles variations in formation water resistivity, R_w, and in shaliness. Any change in R_w is reflected similarly into both the computed R_xo/R_t and the SP amplitude. Thus, comparing the two curves still permits formation-fluid identification. Shaliness also affects the two curves in a similar manner. All other things remaining constant, shaliness reduces the R_xo/R_t value and the SP amplitude. Finally, the R_xo/R_t quick-look technique does not require porosity data, nor use of any F – ϕ relationships.

Fig. 5 is an example of a shaly gas sand at 3,760 through 3,788 ft and several water-productive sands with varying amounts of shaliness. The productive-gas sand is identified by the separation between the R_xo/R_t and SP curves. Water-productive zones are shown by lack of separation. In shaly water zones, the variation in the SP curve is essentially the same as the variation in the R_xo/R_t ratio—a result of the same shale. Therefore, the comparison is not significantly disturbed by shaliness. Neither is it disturbed by variations in R_w.

·        

Fig. 5 – Examples of R_xo/R_t quick-look curve used for comparison with SP to identify zones with movable hydrocarbons.

Estimates of water saturation and saturation ratio in clean formations can be made by comparing the R_xo/R_t and SP curves. Eq. 17 permits S_w/S_xo to be estimated, and then Eq. 12 allows S_w to be estimated.

Nomenclature