Rotational motion, vorticity field

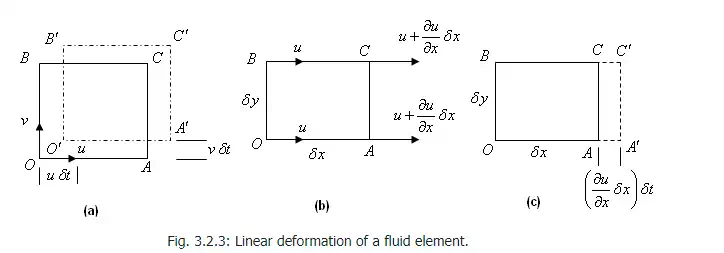
In order to illustrate this concept, we consider a typical fluid element of certain volume at any arbitrary time as shown in Fig. 3.2.1. After certain time interval, it has moved and changed its shape as well as orientation drastically. However, when we limit our attention to an infinitesimal particle of volume 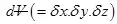at time t and 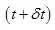within the fluid element, it may be observed that the change of its shape is limited to only stretching/shrinking and rotation with its sides remaining straight even though there is a drastic change in the finite fluid element. Thus, the particle motion in a fluid flow can be decomposed into four fundamental components i.e. translation, rotation, linear strain and shear strain as shown in Fig. 3.2.2. When the fluid particle moves in space from one point to another, it is referred as translation. Rotation of the fluid particle can occur in any of the orthogonal axis. In the case of linear strain , the particle's side can stretch or shrink. When the angle between the sides of the particle changes, it is called as shear strain .

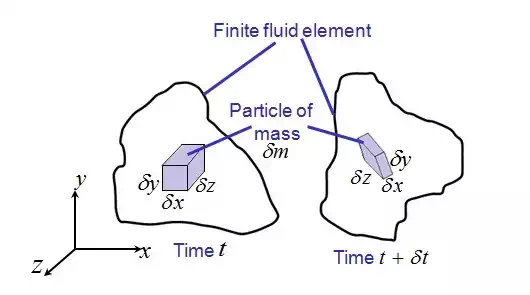
Schematic representation of motion of finite fluid element and infinitesimal particle mass at two different time steps.

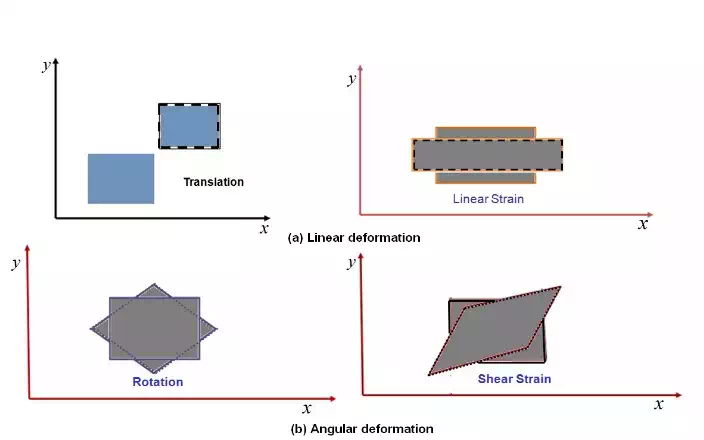
 Basic deformations of fluid mass: (a) Linear deformation; (b) Angular deformation.

In an incompressible fluid, the volumetric dilatation rate is zero because the fluid element volume cannot change without change in fluid density.