Motion of an infinitesimal fluid particle

Imagine an infinitesimal rectangular fluid particle of fixed identity in a flowing fluid. Its sides dx, dy and dz are parallel to the coordinate axes. Let one of its

corners at a given instant be the arbitrarily chosen point P, determined by its position vector i. We shall investigate the velocity field at the same instant in the

infinitesimal neighborhood of point P. Let the position vector of the opposite corner P' of this rectangular particle be i+di. The velocity at point P is 5, while

at point P' it is d + dd. Then a Taylor-series expansion yields for the velocity at the neighboring point P':

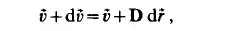
where D is the derivative tensor of the velocity field

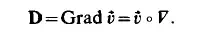
As for any second-order tensor, the derivative tensor can be divided to a symmetric and a skew-symmetric part:

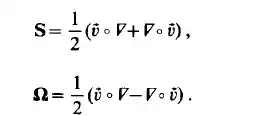
Thus the infinitesimal change in velocity can be written as:

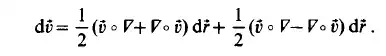
The skew-symmetric part can be decomposed further and expressed by its vector invariant:

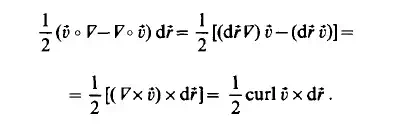
As is well-known the angular velocity of a rotating rigid body is given by

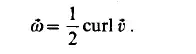
Thus the skew-symmetric part of Grad 6 can particles. For this reason Q is called the vorticity (2.20) be related to the curl of fluid tensor of the flow.

Its matrix can be written easily based on its binary form:

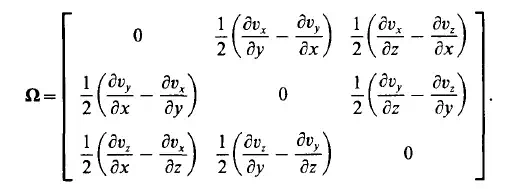
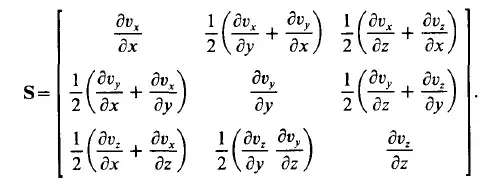
Since the tensor is symmetric it contains six independent quantities. Its principal diagonal represents the three linear strain rates. Their sum is the first scalar invariant of the deformation tensor. It can be seen that this is the divergence of the velocity field which is a measure of the rate of change of dilation

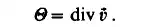
The three other symmetric element pairs express the rate of change of the distortion; in other words the rate of shear deformation. They have special importance

for the construction of constitutive equations. Truesdell has pointed out, that angular velocity is not the most comprehensive measure of the vorticity of any motion. He proposed to introduce a dimensionless parameter, the Truesdell number

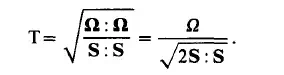
For irrotational flows R=O, but S#O. In this case T=O. For a rotating rigid body S = 0, R # 0, thus T = 0. For the pure translation of a rigid body T = O/O, an indeterminate expression. In general all fluid flows can be characterized by a Truesdell number within the range OST<oo.