The acceleration field

The acceleration is the rate of change of the velocity experienced by a moving particle. It can be expressed as the time derivative of the velocity:

Acceleration vectors form an acceleration field, which can be determined from the velocity field directly by using Eq. (2.11). The vector differential of the velocity

field is:

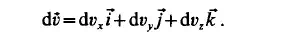
Since the velocity components are scalar point functions of four variables, their differentials are:

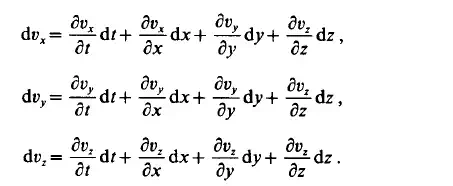
Substituting into Eq. (2.11) and taking into account Eq. (2.2), we obtain the equations:

This can be written in a more simple form as

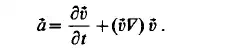
The second term of Eq. (2.12) can be expressed as a dyadic product:

This dyadic or outer product of the two vectors 6 and Vdetermines a tensor of second order

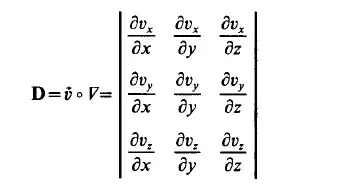
which is called the tensor derivative or the gradient tensor of the velocity field. Thus we may use the following notation:

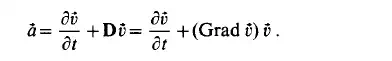
It is obvious that the acceleration is the material derivative of the velocity field. In each of the above expressions for the acceleration field, a local and a convective

component may be separated. The first term aC/at is the local acceleration. It represents the change in the velocity field apparent to an observer fixed in the spatial coordinate system. If the local acceleration component vanishes, i.e.

the flow is steady. The second term is the convective acceleration. It represents the acceleration which, in a steady motion coinciding with 17 at time t = 0, is necessary to direct the particles along their appointed paths at the required velocity. Thus convective acceleration occurs because the fluid particles move in an inhomogeneous velocity

field. It is obvious, that though during steady flow the local acceleration vanishes, the convective acceleration is not necessarily zero, and thus the material acceleration

is also not zero. The convective acceleration vanishes if the velocity field is homogeneous in the direction of the motion. Such a case is that of one-dimensional flow

of an incompressible fluid in a pipe of constant cross-section. A very interesting problem is represented by a sudden change in the velocity field, for example the flow induced by the motion of the piston of a reciprocating pump. Then only instantaneous local acceleration occurs; the convective component develops at a later stage, when the local acceleration generates inhomogeneities in the velocity field. An important parameter was introduced by Szebehely, to measure the unsteadiness of a flow. It illustrates the relative importance of the local and convective accelerations:

For a steady motion without acceleration (steady flow of an incompressible fluid in a pipe or duct of constant cross-section). Szebehely’s number is an indeterminate

expression of the type O/O. If the flow is steady, but the velocity field is inhomogeneous (for example in a diffuser), u=O. For a transient flow in a pipe of constant

cross-section (for example in the case of waterhammer), 01 = cc.