The velocity field
In contrast to the Lagrangian description, the Eulerian treatment does not trace individual particles in the flow. It rather describes what happens at every fixed
point in the flow space as a function of time. At any instant of time there are, at every point of the fluid flow, velocity vectors with a definitive length and direction.
This set of velocity vectors forms the velocity field. The point function of four variables (x, y , z, t) which determines the velocity distribution in space and time can be expressed as
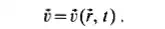
Its scalar components are:

Each scalar component of the vector point function of the velocity field is a scalar point function of four variables. Consider the vectors fi to be bound vectors fixed to the position vector i. Streamlines then are instantaneous curves in the velocity vectors. The concept of streamlines is sufficient for a complete understanding of the flow and for the interpretation of visual observations. The absolute value of the velocity can be characterized by the density of streamlines: the number of streamlines intersecting
a unit surface perpendicular to them is proportional to the magnitude of the velocity. Velocity vectors are the tangent vector to the streamlines at all ordinary points. Figure 2.5 shows the flow pattern developed around a flat plate in a uniform flow. The term “flow pattern” refers to the set of streamlines in the observed region. In the vicinity of the two edges of the plate the streamlines are more densely
packed, reflecting the greater velocity values.

The differential equation defining a streamline can be written as
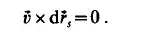
Since the element of arc length along a streamline is parallel to the velocity, their vector product must be zero. The components of this vector product can be determined from the following determinant:
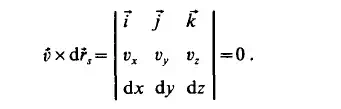
The result is
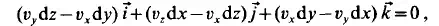
or in another form:
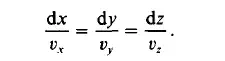
When integrating this equation the time t is taken as a parameter, thus such an integration yields a “snapshot”. The shape of streamlines generally changes with time.
Path lines
A path line is the trajectory of a fluid particle of fixed identity. The description of the paths of individual fluid particles is a characteristic example of the Lagrangian
method. This problem is inherently different from that of the determination of streamlines. To determine path lines based on the velocity field we must solve the
differential equation
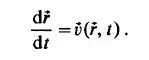
We may take i ( 0 ) = R’ as a boundary condition. Thus we obtain the system of scalar differential equations:
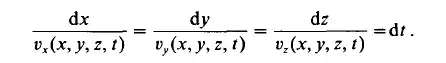
In this system of equations the coordinates x, y, z are unknown functions of the time t , if the values X , Y, 2 corresponding to t = 0 are fixed. A comparison of Eqs
(2.5) and (2.7) shows the essential difference between them; thus streamlines and path lines do not in general coincide. There is an exception: the case of steady flow.
Then the parameter t is eliminated, and the shape of the streamlines and path lines is the same and unchanged with time.
Stream surface, stream tube
Consider an arbitrary curve L in the velocity field. The set of streamlines passing through this curve L form a stream surface (Fig. 2.6). The velocity vector is
perpendicular to the surface normal vector at every point of the stream surface. This can be formulated as

Since the velocity vector has no normal component on the stream surface, there is no flux across it. Thus a solid boundary of a rigid or a deformable body can be
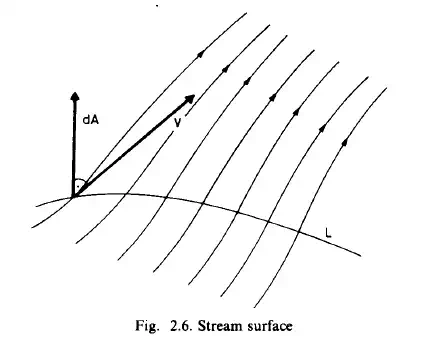
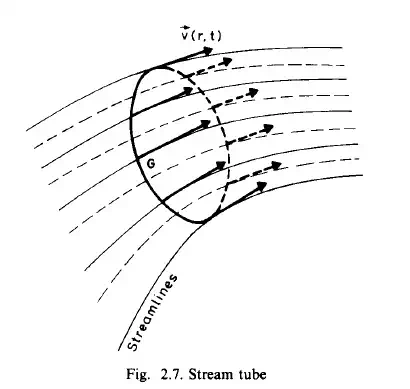
replaced by a stream surface. This boundary surface may be stationary e.g. a wall, or may be moving, e.g. a bubble in a water flow. Consider now a closed curve (G) in the velocity field 6(?, t). The streamlines passing through this closed curve form a stream tube. Since the surface of the stream tube is a stream surface, it is impervious to the fluid. This is shown in Fig. 2.7. The impervious walls of the tubes can be replaced by stream tubes. Thus the boundary condition can be expressed by the equation
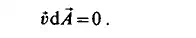
Planar flow
If the flow is the same in all planes parallel to a fixed xy plane and the velocity has no z-component, the motion is called planar flow:
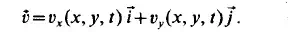
The stream surfaces of the planar flow are planes parallel to each other with congruent flow patterns. The investigation of planar flow can be carried out using simpler mathematical methods than required for three-dimensional flows. Thus three-dimensional flows are often approximated by a set of planar flows. Important properties of the velocity field are obtained from its divergence and curl. If the divergence of the velocity field vanishes
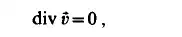
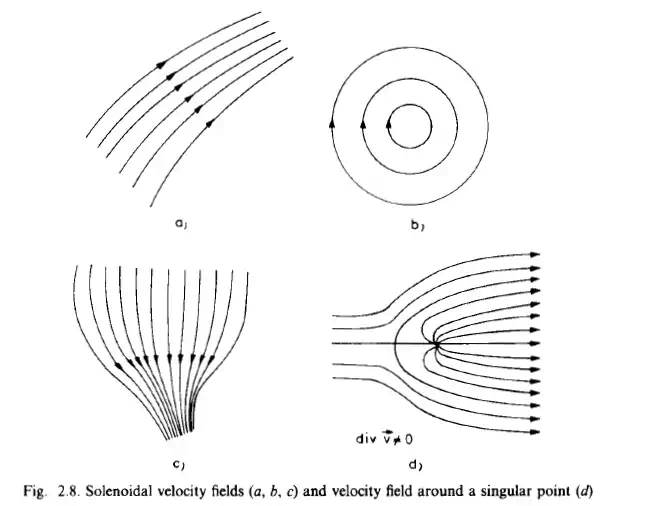
the vector field 6(?, t ) is solenoidal. In a solenoidal velocity field a streamline does not originate from a point nor does it terminate at a point. As shown in Fig. 2.8,
streamlines of solenoidal velocity fields can extend from infinity to infinity (a), or can close onto themselves (b), or end on the boundary surface of the fluid (c). If
the divergence of the velocity field does not vanish, there must be a source (or sources) of the velocity field. Such a source may be located at discrete points. At
such a point, a number of streamlines originate, depending on the strength of the source (d). Sources may be continuously distributed along a line, on a surface or
even throughout a region. This latter condition pertains to compressible fluid flows. The curl of the velocity field is obtained as
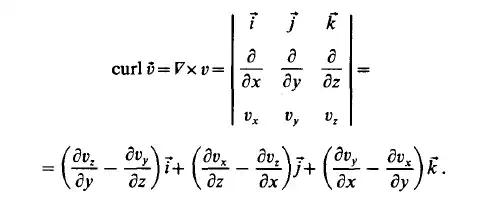
The curl of the velocity field is itself a vector field:
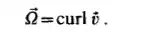
If the vector field of sz' does not vanish, the motion of the fluid particle is the so-called vortex motion. The axial vector b is called the vorticity vector; its direction is the axis of spin, and its magnitude SZ is the strength of vorticity which is proportional to the angular velocity. If the curl of the velocity field vanishes, i.e.
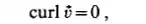
the flow is irrotational. For irrotational flows a velocity potential @ exists of which the velocity components can be determined.