Shock surfaces

It is a rather common phenomenon that abrupt changes occur at the bounding surface of a fluid mass. This happens for example when starting a pump or a compressor, or while opening or closing a valve. The abrupt change in the variables of flow at the boundary disturbs the equilibrium or the previously established flow pattern of the fluid. This disturbance propagates throughout the entire fluid mass. The need for understanding such phenomena arises in a wide variety of engineering problems, for example gas outbursts, waterhammer in pipelines, and the noise of turbomachines or nozzles. The same basic physical principles underlie all of these wave phenomena. Thus it is necessary to introduce a treatment of these phenomena in which will combine the scientific and practical aspects of shock wave phenomena.

Weak and strong singularities

Disturbances which propagate wavelike in a continuum represent singularities of the set of functions of the flow and the variables of state of the medium. These singularities can be distinguished both from the point of view of their mathematical formalism and their physical meaning. A weak singularity is a surface across which the flow variables themselves are

continuous, but certain derivatives of these variables are discontinous between the two sides of the surface. Sound waves are small disturbances with infinitesimal or very small amplitudes in a compressible medium. They form weak singular surfaces.

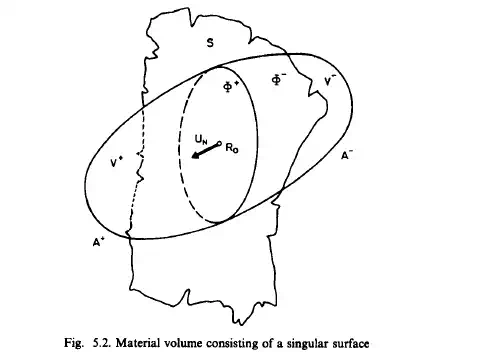
A surface is termed a strong singularity with respect to any variable of flow or state if across it both the continuous set function and its derivative undergo a finite discontinuity. A shock surface in a compressible medium is an example of such a strong singularity. A strong disturbance in a compressible medium propagates with a considerable amplitude. Under certain circumstances shock surfaces develop from these waves of considerable amplitude. The mechanism of generating shock  waves may be illustrated in the following. The amplitudes of the velocity, pressure

and density-disturbances are negligibly small relative to their values at equilibrium. Thus the speed of sound may be considered to remain constant over a wave period. Let us expand the well-known equation for the speed of sound into a Taylor series

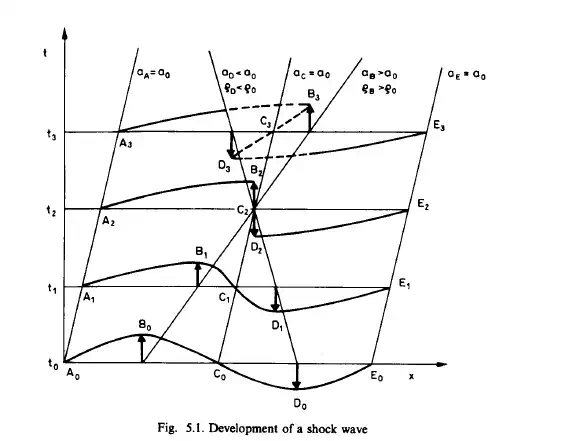
more and more during the course of propagation. It can be seen that the characteristic lines are inclined more during the compressional period and they would eventually cross leading to the situation at the instant t,. The regions of compression  are steepening while the regions of expansion are flattening. The situation at t = t , is obviously impossible since three different values of the density cannotsimultaneously occur at a given point such as xj. Actually, before this happens, or even before the situation t = t, arises, the gradients of the velocity and the temperature during the period of compression become so great that the conductive transport of momentum and the transfer of heat are no longer negligible. These produce a diffusive action which counteracts the steepening tendency. The two  opposing effects achieve a balance; the compressive stage of the wave reaches a steady state, propagating without further distortion. It is then a shock wave. The thickness of the shock-wave front is very small; approximately equal to the free path of the molecules of the gas. In this thin region, the gradients of the flow

variables are extremely large. It may be a suitable approximation to consider this very thin layer of large variations to be a singular surface which contains the discontinuities of the flow variables: velocity, density, and pressure.