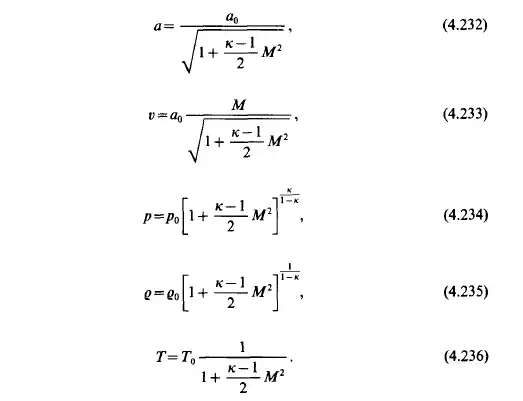High velocity gas flow in pipes with friction

The following discussion deals with the case of a relative high velocity gas flow through a perfectly insulated adiabatic pipe. The pipe has a constant, but not necessarily circular cross-section. The term, ,,relative high velocity gas flow” will be used in the sense of a compressible flow with a velocity greater than 50 m/s. The flow may be either subsonic or supersonic. The flow system is adiabatic, but the flow is not isentropic because of the friction. Since the velocity is relatively high, the flow must be turbulent (see Chapter 7). The only important consequence of this for the present investigation is that the velocity at any cross-section of the pipe is considered to be constant. The flow is steady, thus the heat capacity of the gas is constant. It is important to remember that for compressible fluids, pressure is not simply the mechanical normal stress, but a well defined thermodynamic variable. Therefore, the drop in pressure is caused not only by the friction of the fluid, but also by the change in the thermal state. It is known that thermodynamic processes affecting gases can be represented by means of relatively simple diagrams, in which complicated functions may be represented by simple, smooth curves. For a non-isentropic process the entropyenthalpy diagram (the so-called Mollier diagram) is a convenient graphical representation. In this diagram the actual physical processes proceed in the direction of increasing entropy. For any gas flow in an adiabatic system the energy equation is of the form

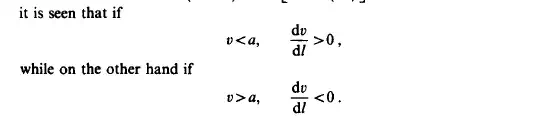
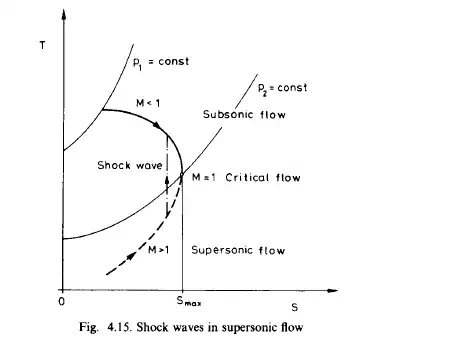
Therefore, a subsonic flow through a duct of constant cross-sectional area will accelerate in the direction of the flow, until the critical velocity is approached. The entropy has a maximum at u=a, thus the subsonic Fanno flow never exceeds the speed of sound. If the ambient pressure is suitably low, a subsonic Fanno flow can reach the speed of sound at the outlet end of the pipe.

A Fanno flow can only be supersonic if it already arrives at the inlet cross-section of the pipe as a supersonic flow. Since the supersonic velocity is greater than the velocity of propagation of any disturbances through the flowing gas, the flow at the inlet is independent of the conditions which prevailed before it reached the inlet. The entropy can increase only to a certain extent, therefore the point representing the gas on the Mollier diagram can proceed only along a Fanno line corresponding to the given mass-flux density, with u approaching the value gaining the maximum