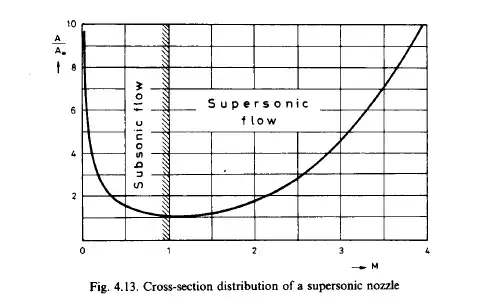
Variation in area for isentropic flow

In many engineering devices used in the natural gas industry, the flow of a gas may be either accelerated or decelerated. Different kinds of orifices and nozzles are used to control the performance of natural-gas producing wells. Nozzles are used in gas turbines to convert internal energy into kinetic energy. For an incompressible flow the relation between the area and the velocity is obvious: an increase in area leads to a decrease in the velocity, and vice versa. It will be shown that for a compressible flow the variation in the area of the flow channel by itself does not determine the nature of the velocity change. The effects of compressibility are most readily illustrated by considering a steady isentropic flow in a channel of variable cross-sectional area. The flow is considered to be one-dimensional: all flow parameters  are taken to be constant across a cross-section perpendicular to the flow. The continuity equation in this case is

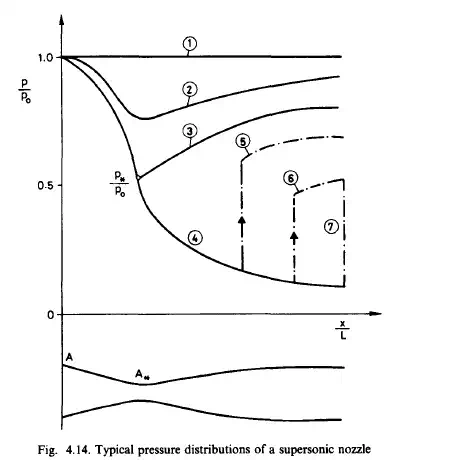
Some typical pressure distributions are shown in Fig. 4.14. If the exit pressure of the nozzle is equal to the stagnation pressure there will be no flow (curve 1). If the exit pressure is slightly smaller than the reservoir pressure, the convergentdivergent nozzle performs like a conventional Venturi tube; the flow is subsonic thorough (curve 2). If the exit pressure is reduced further, the critical velocity and pressure are reached at the throat, as curve 3 shows. In this case the velocity reaches the critical sonic velocity at the throat but cannot be supersonic thorough the

diffuser. The minimum pressure which can occur in the nozzle is represented by the end of curve 4. For the exit pressures that lie between p3 and p4 there are no isentropic solutions. This implies that at intermediate exit pressures some type of non-isentropic process must occur somewhere along the flow. For an inviscid flow the only possibility is the occurrence of shock waves in the supersonic region. The pressure jump which accompanies such a shock is represented by curve 5. After the shock the supersonic flow reverts to subsonic flow, resulting in the exit pressure p s . As the exit pressure decreases, the shock moves downstream as represented by curve 6. At some exit pressures, such as p,, the shock occurs outside the nozzle. With a further decrease of the exit pressure the flow through the nozzle is no longer affected, only the character of the shock waves in the outflowing jet will change.