Eulerian and Lagrangian description of fluid motion

Fluid flow is the characteristic form of motion of fluid continua, an intuitive mechanical concept based on direct experimental observations. Mathematically it means the continuous transformation of three-dimensional Euclidean space into itself. This transformation is an infinite set of one-parameter families of deformations with respect to the real parameter t: time. The initial instant r = O can be totally arbitrary, and the values of the parameter t can range continuously across

the interval

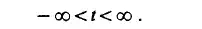
The continuity of time is given by the axiom of continuity: the motion has continuous partial time derivatives of as many orders as needed. For most mechanical

investigations, partial derivatives of the first and second order are sufficient. In continuum mechanics two types of descriptions of motion are possible. These

are called the material, or Lagrangian, and the spatial, or Eulerian, descriptions.

The material or Lagrangian description

The material description is an immediate extension of the method of point-mass mechanics. Fluid particles are considered to represent individual point masses and

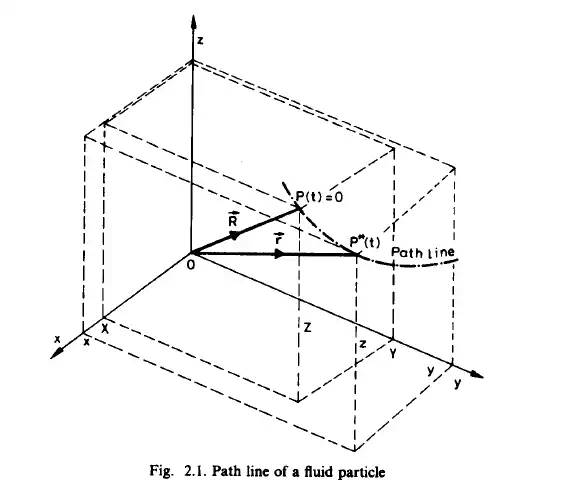
the paths of these particles are traced in the fluid flow in order to formulate the orthogonal coordinate system, which is shown in Fig. 2.1. Naturally it could also

be curvilinear, but for now a rectangular Cartesian coordinate system is chosen. Let the particle under consideration be at the point P given by the position vector

d(X, Y, Z) at the time t = O . At time t, this particle will occupy the position P*, given by the position vector i ( x , y, 2). In this case the vector

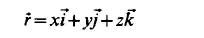
is determined as a function of both the vector

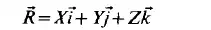
and of the time t , and the flow is represented by the transformation

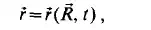
of which the scalar components are:

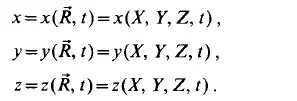
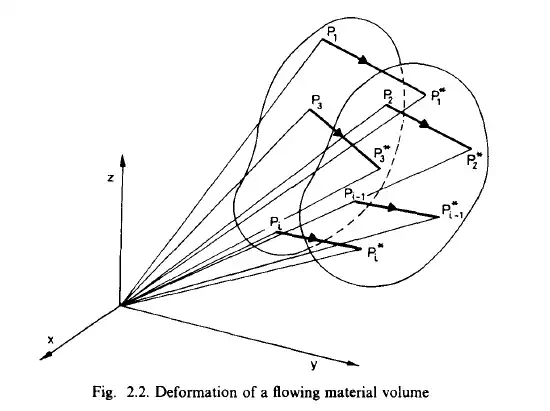
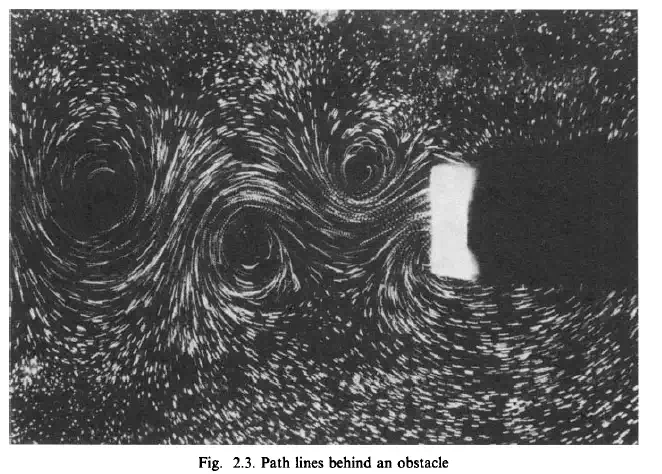
If 8 is kept fixed, while t is varied, Eq. (2.1) determines the path of the particle P, as shown in Fig. 2.2. If the time t is kept fixed, Eq. (2.1) determines the transformation of the region initially occupied by the fluid into its position at time t. Let us assume that the initially distinct points remain distinct during their entire motion. This means that any closed surface moving together with the fluid continuum separates the fluid on both sides of it completely and permanently. This is shown in Fig. 2.2. Both of these methods can be used in the visual observation of the flow. An example for the first method would be a photograph taken with backlighting with a long exposure time, as shown in Fig. 2.3. Here very fine aluminium powder was added to the flow, thus making it possible to observe the flow path of the particles. Figure 2.4 demonstrates the second method and shows

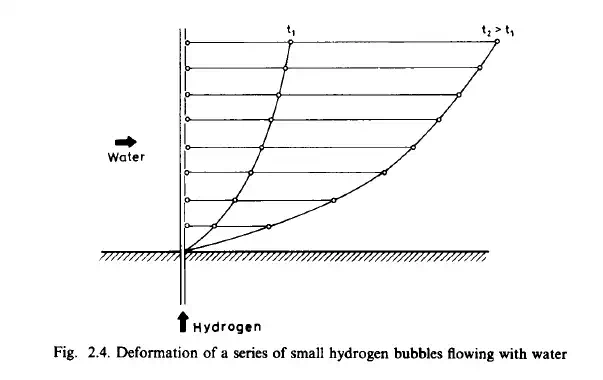
the deformation of a line of small-sized hydrogen bubbles flowing with water at two different instants in time. The inverse of the transformation can be defined as

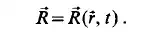
To characterize the motion of a particle defined by the initial coordinates X , Y, The velocity B of the particle is defined as Z, we obtain expressions of the form familiar from point-mass kinematics

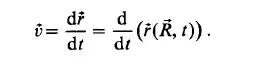
Its components in the directions of the coordinate axes are:

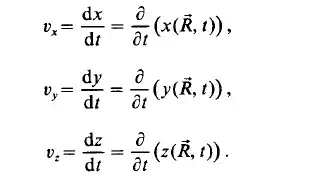
It is obvious that B is a function of certain material variables which relate to the chosen individual fluid particle. These time derivatives expressed in terms of

Lagrangian variables are called material, or substantial derivatives.

The Eulerian or spatial

Description

D’Alembert and Euler were the pioneers of the spatial description of flow. Instead of the observation of individual fluid particles in the flow, they introduced the concept of the velocity field to describe the state of motion at any given point during the course of time. The velocity field is a function of position and time, and gives the velocity of a particle at a position i at a time t. The velocity and other flow variables are not related to a given particle of fixed identity, but to a given point in space, which happens to be there. Studying the evolution of such a function in space and time is much more informative, than the hopeless effort of tracing the path of an infinite number of individual particles. The material, or Eulerian description replaces the flow variables which relate to the particles of the continuum, with the continuous distribution functions of these

quantities. The density or the pressure is given by the scalar functions

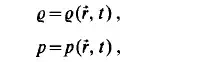
while the velocity or the acceleration is obtained from the vectorial functions

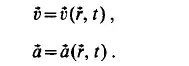
Classical field theory is a sufficient mathematical formalism to express Euler's conception: the motion can be directly described by means of partial differential

equations relating the quantities e, p , 8, 6, etc. By means of Eq. (2.1) and its inverse, any quantity which is the function of the spatial variables i, t is also a function of the material variables d, t and conversely. If we wish to replace the material variables by spatial ones we must solve Eq. (2.1) for the unknowns X , Y, Z expressing them in terms of x, y , z. Substituting these into Eq. (2.2) we obtain the velocity in Eulerian form. To replace the Eulerian description of flow by the Lagrangian one, it is necessary

to take the time integrals of the scalar components of Eq. (2.3):

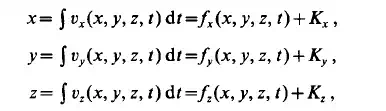
in which K,, K,, K, are constants of integration.

Solving this system of equations for the coordinates x , y , z , we obtain:

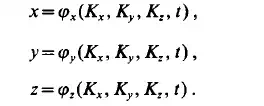
If the constants of the integration are regarded to be Lagrangian variables, these equations determine the motion of the fluid particle initially situated at the point

X=K,, Y=K,,, Z=Kz.

This integration procedure is not easily carried out because of mathematical difficulties. A particularly interesting example of the integration was demonstrated

by Maxwell.