The balance of angular momentum

The principle of conservation of angular momentum belongs to the axioms of mechanics. In spite of its general validity it has been largely neglected in textbooks written for petroleum engineers. The treatment of the equation for the balance of angular momentum is usually restricted to the verification of the theorem of symmetry of the stress tensor. Nevertheless the balance of angular momentum equation is of great value in solving flow problems where torques are more significant than forces, e.g. in turbomachinery as it is shown in CsanPdy’s excellent book. The principle of conservation of angular momentum states that the rate of change of angular momentum of a material volume of fluid V equals the resultant torque exerted by any external forces on this volume of fluid. In order to discuss this statement in more detail, consider an arbitrary material volume V bounded by the closed surface (A), which is moving with the fluid. Let i denote the position vector of an arbitrary point within the volume. At this point the infinitesimal mass

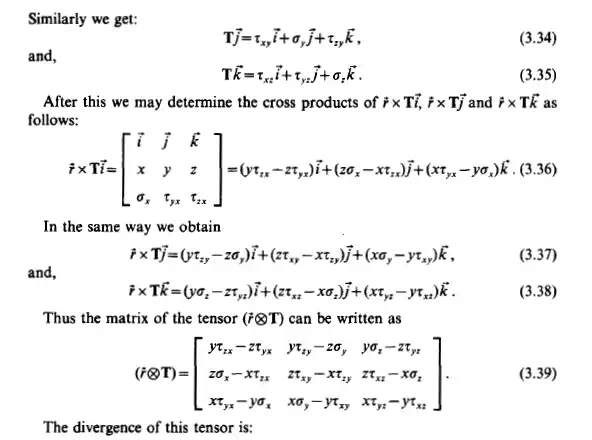
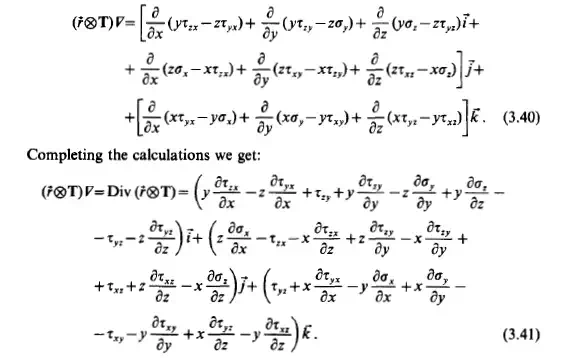
This means that the stress tensor is symmetric if the flowing fluid satisfies the continuity equation, the momentum equation and the angular momentum equation.

The postulate of the symmetry of the stress tensor is equivalent to the determination of three scalar functions from three scalar eqations. If the stress tensor is symmetric the momentum equation and the angular momentum equation are not idependent, one of them may be chosen to solve a flow problem, the other is replaced by the postulate of symmetry.