The balance of momentum

Newton’s second law of motion is perhaps the most important statement in the field of dynamics. As is well-known this states that the rate of change of the momentum of a body equals the sum of the external forces acting on it. To apply this law to a flowing material fluid system consider the volume V, bounded by the simple closed surface ( A ) , made up of the identical particles of fixed identity. The momentum of an infinitesimal volume element of the fluid is QBdV. Since the momentum is an extensive flow variable, the total momentum of the mass of fluid under consideration is the integral of the infinitesimal momentum over the material

tive momentum flux which crosses the bounding surface of the fluid mass. On the right-hand side the first term represents the resultant body force while the second

one represents the resultant of the surface forces acting on the bounding surface. The balance of momentum equation may be rewritten in differential form. Its surface integrals may be transformed into volume integrals by means of the divergence theorem. We first apply this to the identity which relates to the convective momentum flux:

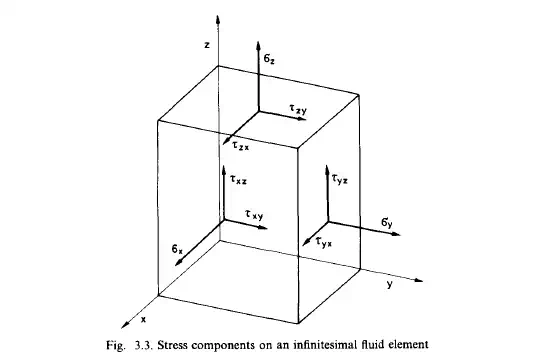
The terms representing the local and the convective momentum flux are easily recognized. In this form the physical meaning of the stress tensor is very obvious:

the stress tensor T represents the conductive flux of the momentum. This conductive momentum flux is transported by virtue of molecular motion, i.e. the continual

random interchange of molecules between adjacent fluid elements produces a transfer of momentum. This phenomenon can be descripted by the laws of probability

and the methods of statistics. From probability distributions it is possible to determine averages or mean values for such parameters as velocity, pressure, etc.

These mean values can then be related to the macroscopically measurable quantities. Molecular motion disperses the momentum. This tendency of equalization

occurs macroscopically as a deterministic process. This is the reason why it is possible to give a phenomenological description of the conductive momentum flux

in a continuum. The idea of a momentum flux without accompanying macroscopic motion may be unfamiliar. Let us consider an example of this from the field of petroleum

engineering. Imagine a pump connected to a pipeline. The pipeline-filling fluid is at rest. Starting the pump, the pressure increases, and the fluid flow accelerates

quickly. Even if the velocity of the flowing fluid is about 1 m/s, the acceleration and the increase in pressure rising propagate as a wave throughout the pipeline with the

speed of sound, some 1000 m/s. As the fluid mass starts to flow faster the momentum is transferred by convection, at the velocity of the flow. In this example the

propagation of the pressure increase and the acceleration is carried out by means of conductive momentum transfer.

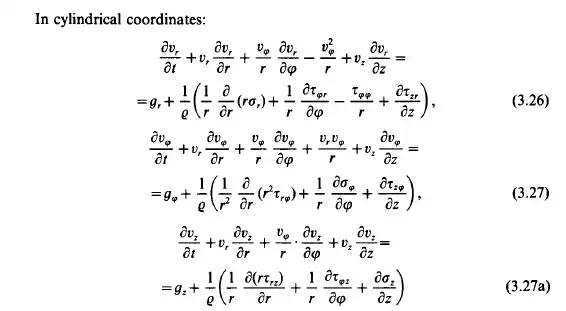
This system of partial differential equations is the so-called stress equation of motion. There are many types of fluids with many different types of stress tensor.

Thus we have equations of motion for inviscid fluids (Euler’s equation), for linearly viscous fluids (Navier-Stokes equation) and further types of equations for the

great variety of non-Newtonian fluids. Invoking the principle of the conservation of mass does not place any restriction on the general applicability of Cauchy’s equation to a homogeneous one-phase flow. In multicomponent systems mass transfer may be important, thus the equation of motion for any phase must be used in the form of Eq. (3.22).