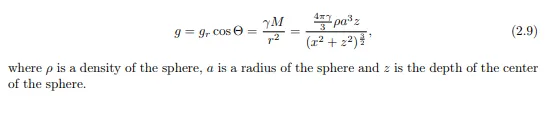
Gravity effect of selected bodies

The simple geometrical bodies are often used for the modelling before the survey is carried out. The aim is to get a rough estimate of the anomaly effect of the target structure. If we, for example, find that the amplitude of a modelled anomaly is lower than sensitivity of our instrument then there is no need to do any measurements at all. . .

Estimating the amplitude and width of the anomaly also enables us to plan a density of profiles and station spacing. For an interpretation at least three stations within the anomaly are necessary. There is a small number of simple basic bodies, however, combining them together can build up even a complex model.

Gravity effect of a sphere A sphere is the most basic body and usually is used as a part of other models or could approximate symmetrical bodies. The gravity effect of a sphere at point P (Fig. 2.8) is:

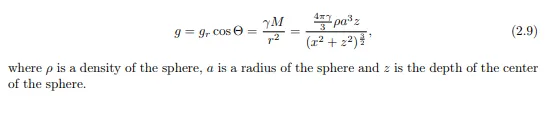
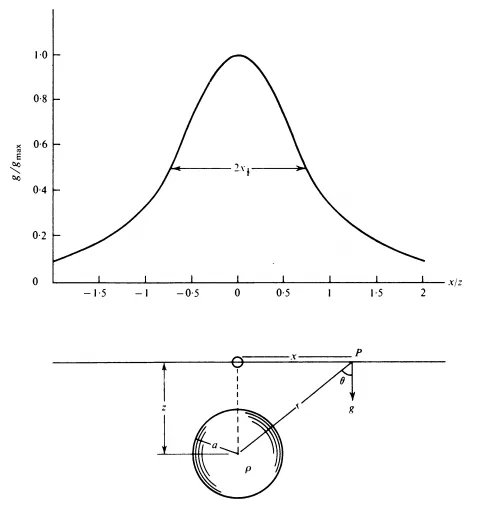
The depth z of the sphere could be estimated from the measured anomaly. When g = gmax 2 then z = 1.3x 1 2 . In other words, the depth of the sphere center could be estimated from the half-width of the anomaly at half of its value (see Fig. 2.8).

Gravity effect of a vertical cylinder The gravity effect on the axis aces of a vertical cylinder is:

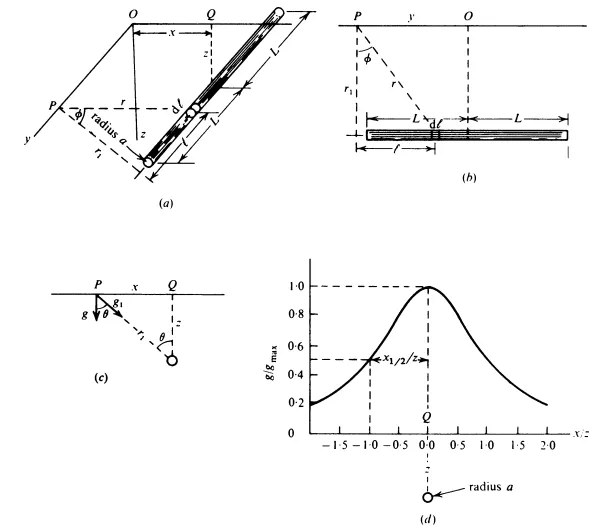
where m is the mass of the rod. If the rod is expanded into the cylinder with a dimension a then m = πa2ρ. When the length L of the rod is infinite (usually a good approximation when the L > 10z then the (2.12) simplifies into the:

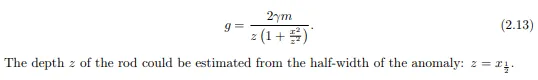
A lot of other geometric bodies could be found in the literature, enabling us to build a complex models. Examples of changes in gravity effect of dofferent bpdies with depth could be found in Figs. 2.10 and 2.11. Two examples of models using the spheres and cylinders are plotted in the Figs. 2.12 and 2.13.

More complex modelling could be done using the computer modelling and irregular bodies. Check, e.g. the Gordon Cooper’s web page at the University of Witwatersrand