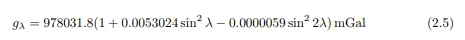
Gravity field of the Earth and data reduction
Because the Earth is not a perfect homogeneous sphere, the gravitational acceleration is not constant over the whole Earth’s surface. Its magnitude depends on five following factors: latitude, elevation, topography of the surrounding terrain, earth tides and density variations in the subsurface. Within the geophysical prospection, we are interested in the last one, which is usually much smaller then the latitude and altitude changes. The removal of unwanted components is often referred to as reduction. Latitude correction. The reason for the latitude correction is two-fold.
First of all, it is caused by the Earth’s centrifugal force being added to the gravitational force (vector sum). This decreases the gravitational force with an increase of a radius of rotation. Hence the smallest gravitational force is on the equator (maximal centrifugal force) and the largest is on the pole. Second, the gravitational force is further affected by the fact that the Earth is not spherical but ellipsoidal. This further decreases the gravitational force on the equator. Both of these effects could be removed by the International Gravity Formula:
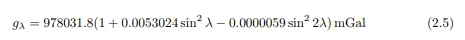
It is clear that the centrifugal force changes only in the N–S direction, not in the W–E. As we have seen from the Newton’s Law of Gravity – equation (2.1) – the gravity decreases with the square of distance. Hence, if we lift the gravimeter from the surface (or any other datum), the gravity will change. To be able to compare data measured in different elevations we have to reduce them to a common datum.
This correction for the topographic effects has several steps. Their description follows. Free-air correction. This is the first step of reducing topography effects. It simply corrects for the change in the elevation of the gravity meter, considering only air (hence a free-air) being between the meter and selected datum (leftmost part of the Figure 2.1). To get the change in gravity acceleration with height we can differentiate the equation (2.4):
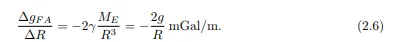
Raising the gravity meter (e.g. extending its tripod) decreases the measured gravity values by 0.3086 mGal/m. Hence to measure with an accuracy of 0.01 mGal we have to measure the elevation of the gravity meter with an accuracy of 3 cm. The free-air correction varies slightly with latitude: Clearly, the sin2 λ and h 2 parts are very small and could be neglected and we end up with the above mentioned ratio. Bouguer correction.
The Bouguer correction removes from the data an effect of rocks laying between the measured point and reference datum (Fig. 2.1 in the centre). This effect was
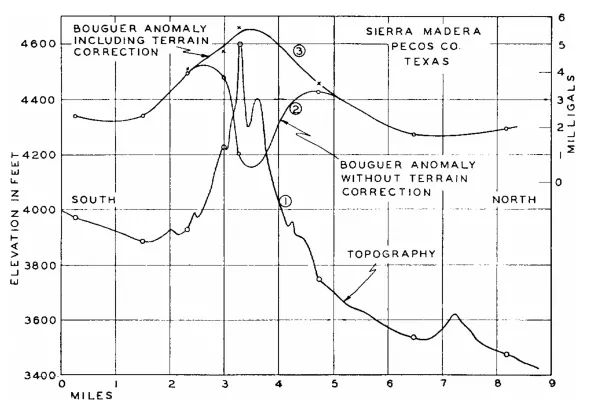

The Bouguer correction assumed the slab to be infinite in the horizontal direction. This is not true, due to a topography and Earth curvature. The correcton for the Earth curvature is used in a large scale surveys and we will leave it out now. The topography correction, however, might be important (Fig. 2.1, right). The hill above the Bouguer slab with its own gravity force pulls in the opposite direction than the Earth, therefore decreasing the measured acceleration (Fig. 2.2). In a similar way, the valley also decreases the value, because when computing the Bouguer correction we have already subtracted the Bouguer slab (with a flat surface) and did not account for the missing masses of the valley.