Archimedes’ principle

Consider now a cube of side d totally immersed in liquid with its top and bottom faces horizontal. The pressure on the bottom face will be higher than on the top by ρgd, and, since pressure is force per unit area and the area of a cube face is d2, the resultant upthrust on the cube is ρgd3. This is a simple example of the so-called Archimedes’ principle, which states that the upthrust experienced by a submerged or floating body is always equal to the weight of the liquid that the body displaces. As Archimedes must have realized, there is no need to prove this by detailed examination of the pressure difference between top and bottom. It is obviously true, whatever the body’s shape. It is obvious because, if the solid body could somehow be removed and if the cavity thereby created could somehow be filled with more fluid instead, the whole system would still be in equilibrium. The extra fluid would, however, then be experiencing the upthrust previously experienced by the solid body, and it would not be in equilibrium unless this were just sufficient to balance its weight.

Archimedes’ problem was to discover, by what would nowadays be called a nondestructive test, whether the crown of King Hieron II was made of pure gold or of gold diluted with silver. He understood that the pure metal and the alloy would differ in density and that he could determine the density of the crown by weighing it to find its mass and making a separate measurement of its volume. Perhaps the inspiration that struck him (in his bath) was that one can find the volume of any object by submerging it in liquid in something like a measuring cylinder (i.e., in a container with vertical sides that have been suitably graduated) and measuring the displacement of the liquid surface. If so, he no doubt realized soon afterward that a more elegant and more accurate method for determining density can be based on the principle that bears his name. This method involves weighing the object twice, first, when it is suspended in a vacuum (suspension in air will normally suffice) and, second, when it is totally submerged in a liquid of density ρ. If the density of the object is ρ′, the ratio between the two weights must be

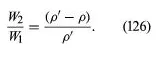
If ρ′ is less than ρ, then W2, according to equation (126), is negative. What that means is that the object does not submerge of its own accord; it has to be pushed downward to make it do so. If an object with a mean density less than that of water is placed in a lake and not subjected to any downward force other than its own weight, it naturally floats on the surface, and Archimedes’ principle shows that in equilibrium the volume of water which it displaces is a fraction ρ′/ρ of its own volume. A hydrometer is an object graduated in such a way that this fraction may be measured. By floating a hydrometer first in water of density ρ0 and then in some other liquid of density ρ1 and comparing the readings, one may determine the ratio ρ1/ρ0—i.e., the specific gravity of the other liquid.

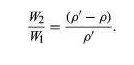
In what orientation an object floats is a matter of grave concern to those who design boats and those who travel in them. A simple example will suffice to illustrate the factors that determine orientation. Figure 2 shows three of the many possible orientations that a uniform square prism might adopt when floating, with half its volume submerged in a liquid for which ρ = 2ρ′; they are separated by rotations of 22.5°. In each of these diagrams, C is the centre of mass of the prism, and B, a point known as the centre of buoyancy, is the centre of mass of the displaced water. The distributed forces acting on the prism are equivalent to its weight acting downward through C and to the equal weight of the displaced water acting upward through B. In general, therefore, the prism experiences a torque. In Figure 2B the torque is counterclockwise, and so it turns the prism away from 2A and toward 2C. In 2C the torque vanishes because B is now vertically below C, and this is the orientation that corresponds to stable equilibrium. The torque also vanishes in 2A, and the prism can in principle remain indefinitely in that orientation as well; the equilibrium in this case, however, is unstable, and the slightest disturbance will cause the prism to topple one way or the other. In fact, the potential energy of the system, which increases in a linear fashion with the difference in height between C and B, is at its smallest in orientation 2C and at its largest in orientation 2A. To improve the stability of a floating object one should, if possible, lower C relative to B. In the case of a boat, this may be done by redistributing the load inside.