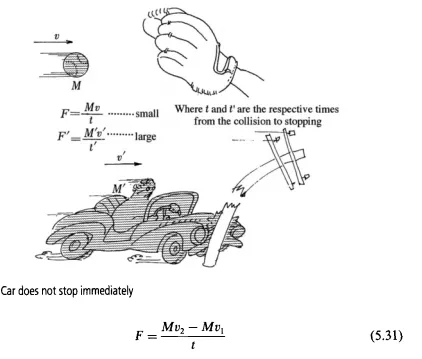
Equation of momentum

A flying baseball can simply be caught with a glove. A moving automobile, however, is difficult to stop in a short time (Fig. 5.16). Therefore, the velocity is not sufficient to study the effects of bodily motion, but the product, Mu, of the mass M and the velocity u can be used as an indicator of the consequences of motion. This is called the linear momentum. By Newton’s second law of motion, the change per unit time in the momentum of a body is equal to the force acting on the body. Now, assume that a body of mass M(kg) will be at velocity u (m/s) in t seconds. The acting force F (N) is given by the following equation:

In other words, the acting force is conserved as an increase in unit time in momentum. This is the law of conservation of momentum. Whenever the reaction force of a jet or the force acting on a solid wall in contact with the flow is to be obtained, by using the change in momentum, such a force can be obtained comparatively simply without examining the complex internal phenomena. In an actual computation, keeping in mind an assumed control volume in the flow, the relation between the change in momentum and the force within that volume is obtained by using the equation of momentum.

In the case where fluid flows in a curved pipe as shown in Fig. 5.17, let ABCD be the control volume, A,, A, the areas, ul, u2 the velocities, and pi, p2 the pressures of sections AB and CD respectively. Furthermore, let F be the force of fluid acting on the pipe; the force of the pipe acting on the fluid is -F. This force and the pressures acting on sections AB and CD act on the fluid, increasing the fluid momentum by such a combined force.' If F, and F, are the component forces in the x and y directions of F respectively, then from the equation of momentum.

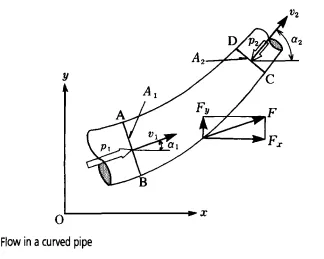
In this equation, rn is the mass flow rate. If Q is the volumetric flow rate, then the following relation exists:

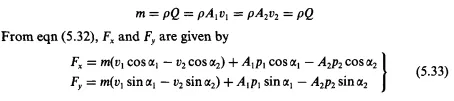
Equation (5.32) is in the form where the change in momentum is equal to the force, but since rn refers to mass per unit time, note that the equation shows that the time-sequenced change in momentum is equal to the force. The combined force acting on the curved pipe can be obtained by the following equation: