Non - Newtonian fluids

Fluids in which shear stress is not linearly related to the rate of shear strain are non– Newtonian fluids. Examples are paints, blot, polymeric solution, etc. Instead of the dynamic viscosity apparent viscosity,  which is the slope of shear stress versus shear strain rate curve, is used for these types of fluid.

Based on the behavior of , non-Newtonian fluids are broadly classified into the following groups

Pseudo plastics (shear thinning fluids):  decreases with increasing shear strain rate. For example polymer solutions, colloidal suspensions, latex paints, pseudo plastic.

Dilatants (shear thickening fluids)  increases with increasing shear strain rate.

Examples: Suspension of starch and quick sand (mixture of water and sand).

Plastics : Fluids that can sustain finite shear stress without any deformation, but once shear stress exceeds the finite stress , they flow like a fluid. The relation between the shear stress and the resulting shear strain is given by

Fluids with n = 1 are called Bingham plastic. some examples are clay suspensions, tooth paste and fly ash.

Thixotropic fluid(Fig. L-2.4):  decreases with time under a constant applied shear stress.

Example: Ink, crude oils.

Rheopectic fluid :  increases with increasing time.

Example: some typical liquid-solid suspensions.

Example                                        

If the equation of a velocity profile over a plate is v = 5y 2 + y (where v is the velocity in m/s) determine the shear stress at y =0 and at y =7.5cm . Given the viscosity of the liquid is 8.35 poise.

Solution :

Surface tension

In this section we will discuss about a fluid property which occurs at the interfaces of a liquid and gas or at the interface of two immiscible liquids. As shown in Fig (L - 3.1) the liquid molecules- 'A' is under the action of molecular attraction between like molecules (cohesion). However the molecule ‘B' close to the interface is subject to molecular attractions between both like and unlike molecules (adhesion). As a result the cohesive forces cancel for liquid molecule 'A'. But at the interface of molecule 'B' the cohesive forces exceed the adhesive force of the gas. The corresponding net force acts on the interface; the interface is at a state of tension similar to a stretched elastic membrane. As explained, the corresponding net force is referred to as surface tension, . In short it is apparent tensile stresses which acts at the interface of two immiscible fluids.

Note that surface tension decreases with the liquid temperature because intermolecular cohesive forces decreases. At the critical temperature of a fluid surface tension becomes zero; i.e. the boundary between the fluids vanishes.

Pressure difference at the interface

In order to study the effect of surface tension on the pressure difference across a curved interface, consider a small spherical droplet of a fluid at rest.

Since the droplet is small the hydrostatic pressure variations become negligible. The droplet is divided into two halves as shown in Fig.L-3.2. Since the droplet is at rest, the sum of the forces acting at the interface in any direction will be zero. Note that the only forces acting at the interface are pressure and surface tension. Equilibrium of forces gives

Contact angle and welting   

As shown in fig. a liquid contacts a solid surface. The line at which liquid gas and solid meet is called the contact line. At the contact line the net surface tension depending upon all three materials - liquid, gas, and solid is evident in the contact angle, . A force balance on the contact line yields:

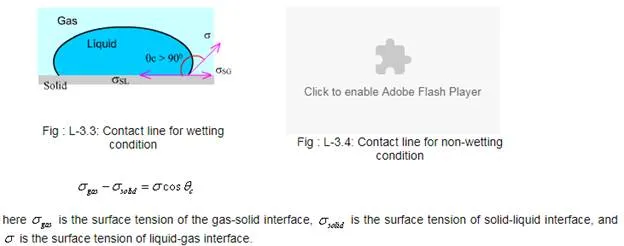
Typical values:

                     for air-water- glass interface

                     for air-mercury–glass interface

If the contact angle  the liquid is said to wet the solid. Otherwise, the solid surface is not wetted by the liquid.