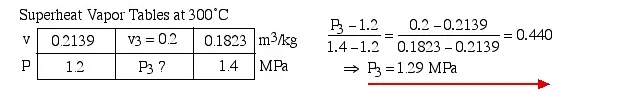
Pure Substances
Phase Change and Property Diagrams
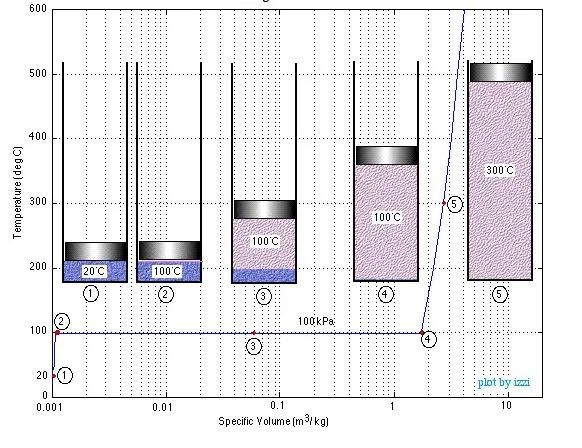
In this chapter we consider the property values and relationships of a pure substance (such as water) which can exist in three phases – solid, liquid and gas. We will not consider the solid phase in this course.In order to introduce the rather complex phase change interactions that occur in pure substances we consider an experiment in which we have liquid water in a piston-cylinder device at 20°C and 100kPa pressure. Heat is added to the cylinder while the pressure is maintained constant until the temperature reaches 300°C, as shown in the following T-v diagram (temperature vs specific volume):

From State (1) to State (2) the water maintains its liquid phase and the specific volume increases very slightly until the temperature reaches close to 100°C (State (2) – Saturated Liquid). As more heat is added the water progressively changes phase from liquid to water vapor (steam) while maintaining the temperature at 100°C (Saturation Temperature – Tsat) until there is no liquid remaining in the cylinder (State (4) – Saturated Vapor). If heating continues then the water vapor temperature increases (T > Tsat) and is said to be in the Superheated (State (5)).
Notice that during this entire process the specific volume of the water increased by more than three orders of magnitude, which made it necessary to use a logarithmic scale for the specific volume axis.
We can repeat this same experiment at different pressures to attain more curves as shown in the figure below.
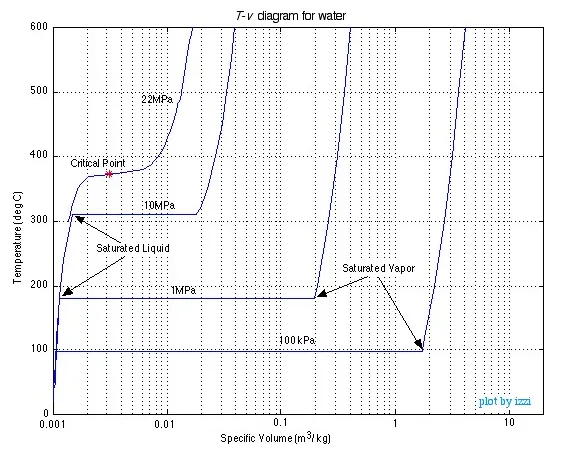
As you can see as the pressure increases the constant temperature region between saturated liquid and saturated vapor becomes smaller and smaller until it is eliminated completely at the critical point, above which there is no clear distinction between the liquid and vapor states.
Saturation lines can be drawn by connecting the loci of the saturated liquid and saturated vapor points as shown in the figure below.
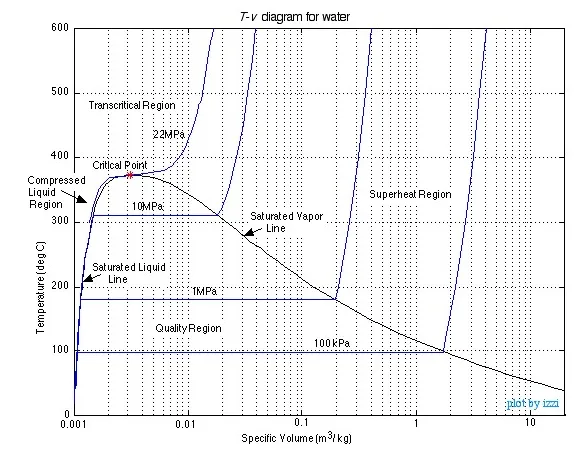
The saturation lines define the regions of
interest as shown in the diagram, being the Compressed Liquid region to
the left, the Quality region enclosed by the saturation lines, and the Superheated
region (which also includes the Transcritical region) to the right of
the saturated vapor line and above the critical point. We will use Property
Tables associated with the regions in order to evaluate the various
properties. Notice that we have provided property tables of steam, Refrigerant
R134a, and Carbon Dioxide, which due to environmental concerns involving R134a
is likely to become the refrigerant of common usage in the future.
The Quality Region, also referred to as
the Saturated Liquid-Vapor Mixture Region, is the area enclosed between
the saturated liquid line and the saturated vapor line. At any point within
this region the quality of the mixture (sometimes referred to as the dryness
factor) is defined as the mass of vapor divided by the total mass of the fluid,
as shown in the following diagram:
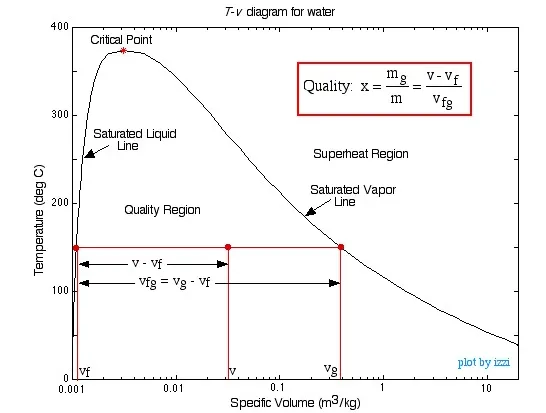
Notice that properties relating to the saturated liquid have the subscript f, and those relating to the saturated vapor have the subscript g. In order to evaluate the quality consider a volume V containing a mass m of a saturated liquid-vapor mixture.
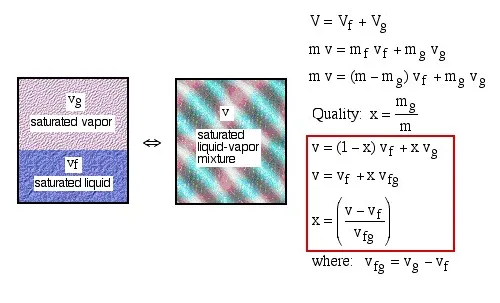
Notice from the steam property tables that we have also included three new properties: internal energy u [kJ/kg], enthalpy h [kJ/kg], and entropy s [kJ/kg.K] all of which will be defined as needed in future sections. At this stage we note that the 3 equations relating quality and specific volume can also be evaluated in terms of these three additional properties.
The above discussion was done in terms of the
temperature (T) and specific volume (v). You may recall from Chapter 1 when we
defined the State Postulate however, that any two independent intensive
properties can be used to completely define all other intensive state
properties. This means we can also evaluate a substance in terms of Pressure
(P) and specific volume (v) as shown below:
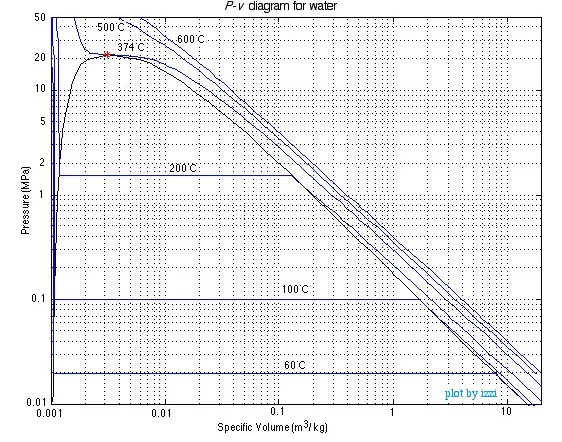
Notice that because of the extremely large range of pressure and specific volume values of interest, this can only be done on a log-log plot. This is extremely inconvenient, so both the T-v and the P-v405 diagrams are normally not drawn to scale, however are sketched only in order to help define the problem, which is then solved in terms of the steam tables. This approach is illustrated in the following solved problems.
Two kilograms of water at 25°C are placed in a piston cylinder device under 100 kPa pressure as shown in the diagram (State (1)). Heat is added to the water at constant pressure until the piston reaches the stops at a total volume of 0.4 m3 (State (2)). More heat is then added at constant volume until the temperature of the water reaches 300°C (State (3)). Determine (a) the quality of the fluid and the mass of the vapor at state (2), and (b) the pressure of the fluid at state (3).
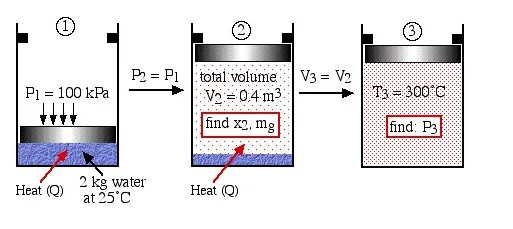
Step 1: Always draw a complete diagram of the states and processes of the problem and include all the relevant information on the diagram. In this case there are three states and two processes (constant pressure and constant volume).
Step 2: In the case of a closed system with a phase change fluid, always sketch a T-v or P-v diagram indicating all the relevant states and processes on the diagram. As mentioned above this diagram will not be drawn to scale, however it will help to define the problem and the approach to solution. In the case of steam, as we determine various values from the steam tables we add these values to the diagram, typically as shown below:
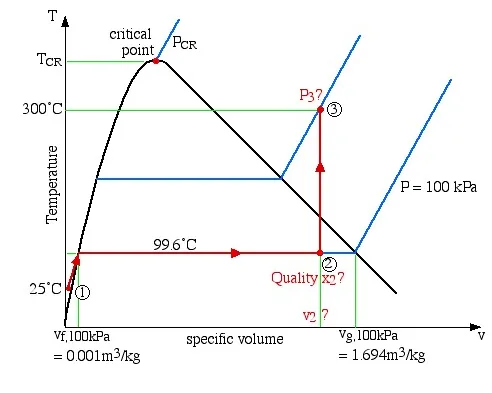
Notice that the T-v diagram is based exclusively on intensive properties, hence mass is not indicated on the diagram. Thus we indicate on the diagram that in order to determine the quality at state (2) we need to first evaluate the specific volume v2, which can then be compared to the saturation values vf and vg at the pressure of 100 kPa.
Thus = = 0.2
Quality
mass of water vapor at state 2:
Concerning state (3), the problem statement did not specify that it is in the superheat region. We needed to first determine the saturated vapor specific volume vg at 300°C. This value is 0.0216 , which is much less than the specific volume v3 of 0.2 , thus placing state (3) well into the superheated region. Thus the two intensive properties which we use to determine the pressure at state (3) are T3 = 300°C, and v3. On scanning the superheat tables we find that the closest values lie somewhere between 1.2 MPa and 1.4 MPa, thus we use linear interpolation techniques to determine the actual pressure P3 as shown below: