PHASE EQUILIBRIUM

Phase equilibrium conditions of a system comprising v components (where v ≥ 1) and φ phases (where φ ≥ 1) results from the Second Law of Thermodynamics and may be expressed by following equalities: temperatures T^(α) (thermal equilibrium, in which there are no heat flows); pressures p^(α) (mechanical equilibrium, i.e., the phases are not separated); chemical potentials  of each of the components (no mass transfer):

(1)

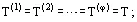
(2)

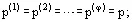
(3)

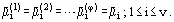
In the presence of force fields, and/or surface tension (which occurs at the phase interfaces) condition (2) needs to be modified.

The chemical potential of a pure substance is equal to the molar (specific) Gibbs energy at the given aggregate state 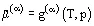. The chemical potential of a component in a mixture is equal to the partial Gibbs energy, which depends on the phase composition of the v-component heterogeneous system:

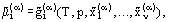
where 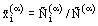 is the mole fraction of the ith component in phase α, where  is the number of moles of the component in phase α and  is the total number of moles of all components in the given phase (α).

(4)

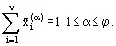
In the v-component, φ phase system there are vφ component fractions . Together with temperature T and pressure p, this gives a total of (vφ + 2) variables defining the (equilibrium) system. However, the equilibria and summation expression (Eqs. (1)-(4)), imply that the variables are not independent and only f variables were.

(5)

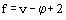
are independent. The f value is called the number of the degrees of freedom (or the variants) of the system. Equation (5) expresses the Gibbs Phase Rule. As soon as f ≥ 0, the number of the phases which are in equilibrium cannot exceed (v + 2) in a v-component system (if a pure substance, then f ≤ 3); a system is called nonvariant if f = v + 2.

For a pure substance, equilibrium of two phases (α and β, say) obeys the condition

(6)

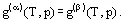
A differential equation of the equilibrium curve follows from (6) if the thermodynamic correlations

(7)

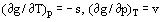
are taken into account; the equation is the well-known Clapeyron-Clausius Equation:

(8)

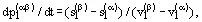
where 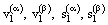 are the molar (specific) volumes and entropies of the coexisting phases. The enthalpy change accompanying the isothermal-isobaric phase transformation α to β is determined by the difference in entropy or enthalpy of the coexisting phases, which are participating in the process transformation:

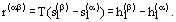
Figures 1-3 present the Gibbs energy dependency on phase temperature gaseous (g), liquid (l), solid (s) phases at three different pressure values. The correlations (Eq. (7)) explain a shape of the curves considering that the entropy should be less for those phases which have a more regular molecular structure; on the contrary, a density for such a phase should be greater, as a rule. Consistent with Eq. (6), the intersection points of the curves define the parameters of the phase transformations at equilibrium: sublimation (s → g), melting (s → 1), evaporation (1 → g). The curves formed by such points are given in Figure 4 often referred to as a phase diagram. If all the lines intersect at the same point, then they give a triple point, with parameters p_tr , T_tr, at which three phases (solid, liquid, and gaseous) exist simultaneously. Triple points of the type s-l-g are inherent to all pure substances except ⁴He; because of quantum effects, the liquid phase of ⁴He forms crystals at higher pressures. As a result, the phase diagram shape essentially differs in comparison with Figure 4. Also, this figure does not present the equilibrium curves and the triple points corresponding to phase transformations which occur between solid states due to allotropic modifications. The slope of the melting curve given in Figure 4 is typical for the majority of the normal substances which obey the correlation v^(l) > v^(s). However, for the case where v^(l) < v^(s) in the vicinity of the triple point of some anomolous substances (for example, water), the slope of the curve is negative (dp_l^(sl)/dT < 0). The vapor-liquid equilibrium curve starts at the triple point and finishes at the critical point T_c, p_c at which liquid and gaseous phases become identical. At supercritical parameters T > T_c, p > p_c. There is no phase transformation of type l → g and the substance is in high density state, which has sometimes been called the fluid state (f).

Figure 1. Phasic Gibbs energy as functions of temperature at pressures above the triple point.

Figure 2. Phasic Gibbs energy as a function of temperature at a pressure between the triple and critical points.

Figure 3. Phasic Gibbs energy as a function of temperature at pressure.

According to the Second Law of Thermodynamics, the stable states of substances at given T and p relate to minimal values of the Gibbs energy g(T,p). An unstable state can only exist transiently. Metastable states may exist indefinitely until some sufficiently strong external influence causes the system to pass into the stable state. Stability of the metastable state diminishes as the parameters of the system depart more and more from the equilibrium state. The metastable states of a superheated liquid (which doesn't boil) and a supercooled liquid (which doesn't form crystals) as well as a supercooled vapor (which doesn't condense) are frequent in practice; these states are represented by lines above the lines which have minimum Gibbs energy as shown in Figures 1 and 2.

The thermodynamic properties ψ of the heterogeneous system— which may be defined as a first derivative of the Gibbs energy with respect to the parameters in Eq. (7)—specific (molar) volume, entropy, enthalpy, etc.— may be calculated by summing the same property ψ^(α) related to the phase under equilibrium

(9)

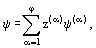
where z^(α) = N^(α) /N is a mass (or mole) fraction of phase α, N is the total number of moles in the system. Of course,

(10)

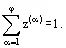
Under equilibrium, for a pure substance, the fraction zα may have any value between 0 and 1 at given p and T subject to these values obeying Eq. (10). An example is the moisture fraction z⁽¹⁾ in the case of vapor-liquid equilibrium. Here, z⁽¹⁾ is referred to as Quality. This type of state of the heterogeneous systems is called indifferent. In such states, as well as at the critical point of pure substances—thermal expansion (∂s/∂T)_p , isothermal compressibility (∂v/∂p)_T, as well as an isobaric heat capacity c_p = T(∂v/∂T)_p —are infinitely large. Also, constant volume values of specific heat capacity c_v = T(∂s/∂T)_v, as well as the derivative (∂p/∂T)_v vary with a jump, when the substance passes from a one-phase into two-phase state; they stay defined in the two-phase region. Figures 4 and 5 illustrate the described situation for pure substances with dependencies of specific volume and entropy on temperature and pressure. The heavy lines relate to borders of the coexisting phases regions, the weak lines are isotherms, and the broken ones are isochores.

If the total composition of the v-component, φ-phase system is given, then it follows that:

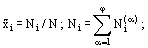
(11)

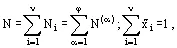
and hence:

(12)

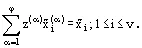
The number of the equilibrium equations together with the material balance equations are exactly equal to the number of the values 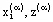, which need to be defined.

Figure 4. Phase diagram in terms of pressure and temperature.

Figure 5. Phase diagram in terms of entropy and temperature.

The thermodynamic behavior of the multicomponent heterogeneous systems is identical to that which has been described above for pure substances. In particular, appearance (or disappearance) of the phase causes a discontinuity in the temperature and pressure dependencies of those thermodynamic functions, which may be defined as the first derivatives of the Gibbs energy (v, s, h, etc.). As to the second derivatives ((∂v/∂T)_p, (∂v/∂p)_T, c_p, c_v, etc.), they change the values in a jumpwise manner. Indifferent thermodynamic states are inherent to azeotropic mixtures and non- or mono-variant multicomponent mixtures.

The number of types of the phase equilibrium is far greater in multicomponent systems in comparison with pure substances. In particular, at certain conditions, some liquids or high-density gases may split into two phases, which have the same aggregate states but different compositions (liquid-liquid or gas-gas equilibria).

The types of phase equilibrium described above relate to the first order of phase change. By contrast, the second order of phase changes (ferromagnetic-paramagnetic, normal conductor— superconductor, normal—superfluid helium, etc.) are not accompanied by volume and heat effects; that is why, in such situations, there are no phase equilibrium states