Gibbs Free Energy and Other Thermodynamic Functions

Dexter Perkins (University of North Dakota), Andrea Koziol (University of Dayton), John Brady (Smith College)

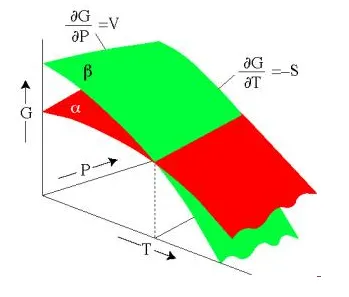
Comparing the Gibbs Free Energy of two minerals, α and β, both with the same composition. The mineral with the lowest Energy is stable. Here we see that α is stable under some P-T conditions, and β is stable under different conditions.

Gibbs Free Energies of Phases

All phases, whether mineralogical or not, have an associated Gibbs Free Energy of Formation value abbreviated ΔG_f. The ΔG_f value describes the amount of energy that is released or consumed when a phase is created from other phases.

Consider, for example, enstatite (MgSiO₃). The Gibbs Free Energy of Formation for enstatite from pure elements (Mg, Si and O) = ΔG_f (enstatite, elements) is about -1,460.9 J/mole at room temperature and pressure. The Gibbs Free Energy of Formation for enstatite from oxides (MgO and SiO₂) = ΔG_f(enstatite, oxides) is about -35.4 J/mole at room temperature and pressure. Gibbs Energy values are, most often today, given in units of joules/mole or (less commonly) calories/mole.

The ΔG_f values given above for enstatite are both negative. This means that enstatite is more stable than, and will form from, the separate elements or separate oxides. Some of the energy produced will be given off as heat; some will contribute to entropy.

Gibbs Free Energies are Relative Values

Gibbs free energies are relative values, not absolute values. They allow us to compare energies of different phases but individual values by themselves have no significance. Because Gibbs Energy values are relative, we can arbitrarily assume some values in order to calculate others. So, by convention the ΔG_f for any pure element is assumed to be as zero.

The Gibbs Free Energy of Reaction

We can calculate the Gibbs Free energy of any reaction by summing the energies of the right-hand side of the reaction and subtracting the energies of the left hand side. For example, we can write a reaction describing the formation of enstatite from separate elements:

Mg + Si + 3O = MgSiO3 (rxn 1)

The ΔG for reaction (1) is the Gibbs Free Energy of formation of enstatite from the elements (-1,460.9 J/mole at room temperature and pressure):

ΔG₁ = ΔG_f(enstatite, elements) = ΔG_f(enstatite) - ΔG_f(Mg)-ΔG_f(Si)-3ΔG_f(O) (Eqn 1)

All reactions have an associated ΔG_rxn value but the values vary with pressure and temperature (T). If we wish to make thermodynamic calculations involving ΔG_f, we must either look the values up in a book for the P-T conditions of interest, or calculate the values using standard equations.

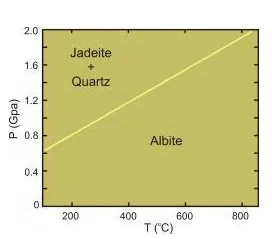
The reaction of Albite to Jadeite + Quartz. At 400° the reaction takes place at about 1.18 GPa.

Determining the Location of Metamorphic Reactions

Consider the reaction: albite = jadeite + quartz (rxn 2)

For this reaction:

ΔG₂ = ΔG_f (jadeite, elements) + ΔG_f (quartz, elements) - ΔG_f (albite, elements) (Eqn 2)
or
ΔG₂ = ΔG_f (jadeite, oxides) + ΔG_f (quartz, oxides) - ΔG_f (albite, oxides) (Eqn 3)

These two values will always come out to be the same, but most reference books list values relative to the elements. If we look up ΔG_f values in a reference book, we will find that:

At 400° C and 1.0 GPa: ΔG₂ > 0
At 400° C and 1.4 GPa: ΔG₂ < 0

So, at 400° C and 1.0 GPa, albite is the stable form, but at 1.4GPa albite will react to form jadeite + quartz. At about 400°C and 1.18 GPa, on the reaction line, ΔG₂ = 0.

For any reaction under a given set of P-T conditions: If the ΔG_rxn < 0, the reaction proceeds to the right. If the ΔG_rxn >0, the reaction proceeds to the left. The univariant reaction curve that separates the two assemblages actually represents the locus of points where ΔG_rxn = 0