Fuels and Combustion

Fuels and Combustion

Most of the fuels contain Carbon and Hydrogen and are in solid, liquid or in gaseous form.

1. Solid Fuels (Coal): Consists of moisture, volatile matter, fixed carbon and ash. The analysis specifies on a mass basis, the relative amounts of these constituents. The ultimate analysis may be given on the dry basis.

2. Liquid Fuels: Most liquid fuels are mixtures of many different Hydrocarbons. Common examples are Gasoline, Kerosene, Diesel oil etc. Commonly a liquid fuel is treated as a single hydrocarbon with an empirical formula C_xH_yeven though it is a mixture of several hydro carbons.

3. Gaseous fuels: Natural gas (mainly Methane), coal gas (a mixture of methane and Hydrogen) etc.

In most of the combustion processes the required Oxygen is not supplied as pure Oxygen but is supplied as air. Air contains 21 mol percent O₂ and 79 mol percent of N₂.

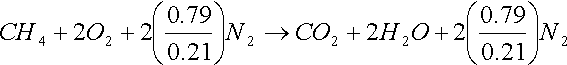
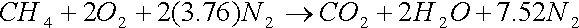
The minimum amount of air which supplies the required amount of oxygen for complete combustion of a fuel is called the stoichiometric or theoretical air.

The amount of air in excess of the stoichiometric air is called excess air. It is usually expressed in terms of the stoichiometric air as percent excess air. Amount of air less than stoichiometric are called deficiency of air.

General combustion reaction

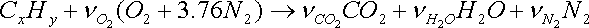
the coefficients to the substances called stoichiometric coefficients. The balance of atoms yields the theoretical amount of air as

C: 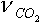= x

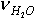H:2=y

N_2: 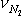=3.76*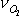

O₂: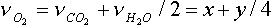

And the total number of moles of air for 1 mole of fuel becomes

n_air =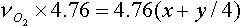

Two important parameters often used to express the ratio of fuel and air are the air-fuel ratio ( AF ) and its reciprocal, the fuel-air ratio ( FA ) .

AF_mass= m_air / m_fuel

AF_mole= n_air / n_fuel

They are related through molecular weight as

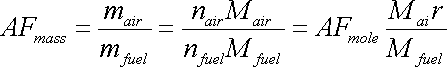
problem:

Methane (CH₄) is burned with atmospheric air. The analysis of the products on a dry basis is as follows:

CO₂�� 10.00%

O₂�� 2.37

CO�� 0.53

N₂�� 87.10

�� -----------

�� 100.00%

Calculate the air-fuel ratio and the percent theoretical air, and determine the combustion equation.

Solution:

The solution consists of writing the combustion equation for 100 kmol of dry products, introducing letter coefficients for the unknown quantities, and then solving for them.

From the analysis of the products, the following equation can be written, keeping in mind that this analysis is on a dry basis.

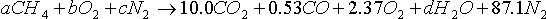
A balance for each of the elements will enable us to solve for all the unknown coeffiecients:

Nitrogen balance: c = 87.1

Since all the nitrogen comes from the air,

c / b =3.76 b=87.1/3.76=23.16

Carbon balance: a = 10.00+0.53=10.53

Hydrogen balance: d=2a=21.06

Oxygen balance: All the unknown coefficients have been solved for, and therefore the oxygen balance provides a check on the accuracy. Thus, b can also be determined by an oxygen balance.

b=10.00+0.53/2+2.37+21.06/2=23.16

substituting these values for a,b,c and d we have

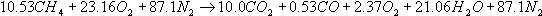
Dividing through by 10.53 yields the combustion equation per kmol of fuel.

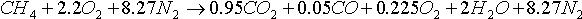
The air-fuel ratio on a mole basis is

2.2+8.27=10.47 kmol air/kmol fuel

The fuel-air on a mass basis is found by introducing the molecular weights.

AF=10.47*28.97/16.0=18.97 kg air/kg fuel

The theoretical air-fuel ratio is found by writing the combustion equation for theoretical air.

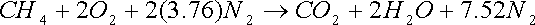
AF_theo= (2+7.52)28.97/16.0=17.23 kg air/kg fuel

The percent theoretical air is 18.97/17.23= 110%

Problem

A particular coal has the following ultimate analysis on a dry basis, percent by mass:

Component	Percent by mass
Sulfur	0.6
Hydrogen	5.7
Carbon	79.2
Oxygen	10.0
Nitrogen	1.5
Ash	3.0

This coal is to be burned with 30% excess air. Calculate the air-fuel ratio on a mass basis.

Solution:

One approach to this problem is to write the combustion equation for each of the combustible elements per 100 kg of fuel. The molar composition per 100 kg of fuel is found first.

Kmol S / 100 kg fuel = 0.6/32 = 0.02

Kmol H₂ / 100 kg fuel = 5.7/2 = 2.85

Kmol C / 100 kg fuel=79.2/12=6.60

Kmol O₂ / 100 kg fuel=10/32=0.31

Kmol N₂ / 100 kg fuel=1.5/28=0.05

The combustion equations for the combustible elements are now written, which enables us to find the theoretical oxygen required.

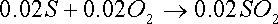
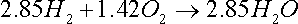
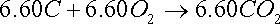
8.04 kmol O₂ required / 100 kg fuel

-0.31 kmol O₂ in fuel / 100 kg fuel

7.73 kmol O₂ from air / 100 kg fuel

AF_theo=[7.73+7.73(3.76)]28.97/100=10.63 kg air/kg fuel

For 30%excess air the air-fuel ratio is

AF=1.3*10.63=13.82 kg air/ kg fuel