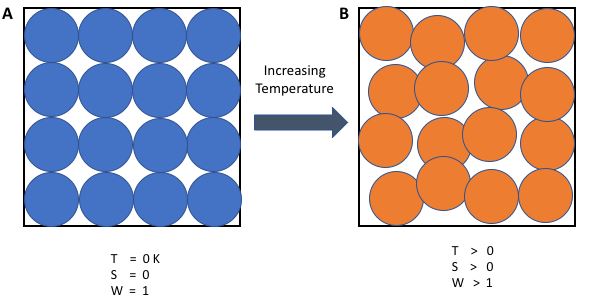
Entropy, denoted by ‘S’, is a measure of the disorder/randomness in a closed system. It is directly related to the number of microstates (a fixed microscopic state that can be occupied by a system) accessible by the system, i.e. the greater the number of microstates the closed system can occupy, the greater its entropy. The microstate in which the energy of the system is at its minimum is called the ground state of the system.
At a temperature of zero Kelvin, the following phenomena can be observed in a closed system:
Therefore, a system at absolute zero has only one accessible microstate – it’s ground state. As per the third law of thermodynamics, the entropy of such a system is exactly zero.

This law was developed by the German chemist Walther Nernst between the years 1906 and 1912.
The Nernst statement of the third law of thermodynamics implies that it is not possible for a process to bring the entropy of a given system to zero in a finite number of operations.
The American physical chemists Merle Randall and Gilbert Lewis stated this law differently: when the entropy of each and every element (in their perfectly crystalline states) is taken as 0 at absolute zero temperature, the entropy of every substance must have a positive, finite value. However, the entropy at absolute zero can be equal to zero, as is the case when a perfect crystal is considered.
The Nernst-Simon statement of the 3rd law of thermodynamics can be written as: for a condensed system undergoing an isothermal process that is reversible in nature, the associated entropy change approaches zero as the associated temperature approaches zero.
Another implication of the third law of thermodynamics is: the exchange of energy between two thermodynamic systems (whose composite constitutes an isolated system) is bounded.
For an isentropic process that reduces the temperature of some substance by modifying some parameter X to bring about a change from ‘X2’ to ‘X1’, an infinite number of steps must be performed in order to cool the substance to zero Kelvin.
This is because the third law of thermodynamics states that the entropy change at absolute zero temperatures is zero. The entropy v/s temperature graph for any isentropic process attempting to cool a substance to absolute zero is illustrated below.
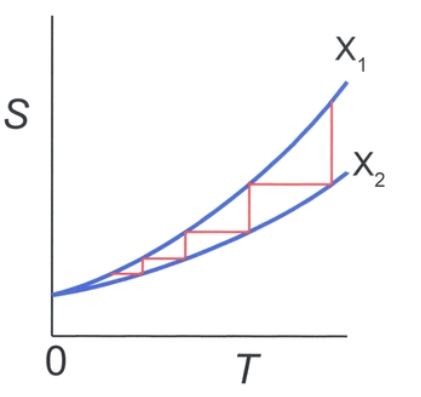
From the graph, it can be observed that – the lower the temperature associated with the substance, the greater the number of steps required to cool the substance further. As the temperature approaches zero kelvin, the number of steps required to cool the substance further approaches infinity.
As per statistical mechanics, the entropy of a system can be expressed via the following equation:
S – S0 = 푘B ln훀
Where,
Now, for a perfect crystal that has exactly one unique ground state, 훀 = 1. Therefore, the equation can be rewritten as follows:
S – S0 = 푘B ln(1) = 0 [because ln(1) = 0]
When the initial entropy of the system is selected as zero, the following value of ‘S’ can be obtained:
S – 0 = 0 ⇒ S = 0
Thus, the entropy of a perfect crystal at absolute zero is zero.
An important application of the third law of thermodynamics is that it helps in the calculation of the absolute entropy of a substance at any temperature ‘T’. These determinations are based on the heat capacity measurements of the substance. For any solid, let S0 be the entropy at 0 K and S be the entropy at T K, then
