Heat capacity and internal energy

The goal in defining heat capacity is to relate changes in the internal energy to measured changes in the variables that characterize the states of the system. For a system consisting of a single pure substance, the only kind of work it can do is atmospheric work, and so the first law reduces to

dU = d′Q − P dV.                                   (28)

Suppose now that U is regarded as being a function U(T, V) of the independent pair of variables T and V. The differential quantity dU can always be expanded in terms of its partial derivatives according to                             (29)

where the subscripts denote the quantity being held constant when calculating derivatives. Substituting this equation into dU = d′Q − P dV then yields the general expression

                  (30)

for the path-dependent heat. The path can now be specified in terms of the independent variables T and V. For a temperature change at constant volume, dV = 0 and, by definition of heat capacity

,d′Q_V = C_V dT.                                                       (31)

The above equation then gives immediately

                                                       (32)

for the heat capacity at constant volume, showing that the change in internal energy at constant volume is due entirely to the heat absorbed.

To find a corresponding expression for C_P, one need only change the independent variables to T and P and substitute the expansion

                                (33)

for dV in equation (28) and correspondingly for dU to obtain

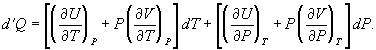 (34)

For a temperature change at constant pressure, dP = 0, and, by definition of heat capacity, d′Q = C_P dT, resulting in

                               (35)

The two additional terms beyond C_V have a direct physical meaning. The termrepresents the additional atmospheric work that the system does as it undergoes thermal expansion at constant pressure, and the second term involvingrepresents the internal work that must be done to pull the system apart against the forces of attraction between the molecules of the substance (internal stickiness). Because there is no internal stickiness for an ideal gas, this term is zero, and, from the ideal gas law, the remaining partial derivative is

          (36)

With these substitutions the equation for C_P becomes simplyC_P = C_V + nR (37)orc_P = c_V + R (38)for the molar specific heats. For example, for a monatomic ideal gas (such as helium), c_V = 3R/2 and c_P = 5R/2 to a good approximation. c_VT represents the amount of translational kinetic energy possessed by the atoms of an ideal gas as they bounce around randomly inside their container. Diatomic molecules (such as oxygen) and polyatomic molecules (such as water) have additional rotational motions that also store thermal energy in their kinetic energy of rotation. Each additional degree of freedom contributes an additional amount R to c_V. Because diatomic molecules can rotate about two axes and polyatomic molecules can rotate about three axes, the values of c_V increase to 5R/2 and 3R respectively, and c_P correspondingly increases to 7R/2 and 4R. (c_V and c_P increase still further at high temperatures because of vibrational degrees of freedom.) For a real gas such as water vapour, these values are only approximate, but they give the correct order of magnitude. For example, the correct values are c_P = 37.468 joules per K (i.e., 4.5R) and c_P − c_V = 9.443 joules per K (i.e., 1.14R) for water vapour at 100 °C and 1 atmosphere pressure.