Gibbs' Phase Rule

Introduction

Minerals are the monitors of the physical and chemical conditions under which they formed. The occurrences of minerals, their parageneses (stable associations), types of reactions, and compositional variation (e.g. zoned minerals) all provide important information about geologic history and processes. Of particular importance to geologists are:

·         Estimates of pressure and temperature (geothermobarometry)

·         Estimates of other physico-chemical conditions such as acidity (pH) and oxidation state (eH)

·         Partial pressures of gases (e.g. fugacities of H₂O, CO₂ , etc.)

·         Partitioning of major and trace elements between phases (e.g. minerals, melts and/or fluids) to characterize and quantify petrogenetic processes; and

·         Use of minerals in geochronology and thermochronology

Gibbs' Phase Rule provides the theoretical foundation, based in thermodynamics, for characterizing the chemical state of a (geologic) system, and predicting the equilibrium relations of the phases (minerals, melts, liquids, vapors) present as a function of physical conditions such as pressure and temperature. Gibbs' Phase Rule also allows us to construct phase diagrams to represent and interpret phase equilibria in heterogeneous geologic systems. In the simplest understanding of phase diagrams, stable phase (mineral) assemblages are represented as "fields" (see colored areas on the figure to the right) in "P-T space", and the boundaries between stable phase assemblages are defined by lines (or curves) that represent reactions between the phase assemblages. The reaction curves actually represent the condition (or the locus of points in P-T space) where ΔG_rxn =0; for more information on this point see Gibbs Free Energy. A solid understanding of Gibbs' Phase Rule is required to successfully master the applications of heterogeneous phase equilibria presented in this module.

Definitions

Gibbs Phase Rule is expressed by the simple formulation:

P + F = C + 2, where

P is the number of phases in the system

A phase is any physically separable material in the system. Every unique mineral is a phase (including polymorphs); igneous melts, liquids (aqueous solutions), and vapor are also considered unique phases. It is possible to have two or more phases in the same state of matter (e.g. solid mineral assemblages, immiscible silicate and sulfide melts, immiscible liquids such as water and hydrocarbons, etc.) Phases may either be pure compounds or mixtures such as solid or aqueous solutions--but they must "behave" as a coherent substance with fixed chemical and physical properties.

C is the minimum number of chemical components required to constitute all the phases in the system

For historical reasons, geologists normally define components in terms of the simple oxides (e.g. SiO₂, Al₂O₃, CaO, etc.). If two possible components always occur in the same proportions in multiple phases in a system, these can be combined into a single component (remember, we are always trying to define the minimum number of components required to make all the phases in the system). Consider the reaction:

CaMg(CO₃)₂ + 2 SiO₂ = CaMgSi₂O₆ + 2 CO₂
Dolomite + 2 Quartz = Diopside + 2 Carbon Dioxide

Normally we would pick the 4 components: CaO, MgO, SiO₂, and CO₂ based on the simple oxides. However, because Ca and Mg are in a 1:1 ratio in both dolomite and diopside (and not present in quartz or carbon dioxide), we can consider this a ternary system with components: CaMgO₂, SiO₂, and CO₂

In some geologic systems it is convenient to define the components in terms of end-member compositions (e.g. binary systems such as carbonates, CaCO₃ - MgCO₃; alkali feldspars, NaAlSi₃O₈ - KAlSi₃O₈, etc.).

In some cases, a given mineral assemblage may be represented by a sub-set of the whole system if fewer components are needed to define the compositions of the observed mineral assemblage--this is known as a degenerate system. A good example of this can be seen on a ternary (3 component) chemographic projection if the phases of interest plot in a co-linear fashion (i.e. requiring only two components to define the phase compositions in what is otherwise a three component system).

A more complete discussion of components can be found in the section on Plotting Mineral Compositions and Chemographic Projections.

F is the number of degrees of freedom in the system (also referred to as the variance of the system).

For geologic applications, this generally refers to the number of variables (e.g. pressure and temperature) that can be independently changed without altering the state of the system (i.e. the number of phases and their compositions are constant). Three common types of equilibria are possible:

·         Invariant equilibria, in which neither P or T can be changed; on a phase diagram, this is represented as a singular invariant point

·         Univariant equilibria, in which either P or T can be changed independently, but to maintain the state of the system, there must be a corresponding change in the other variable; on a phase diagram this is referred to as a univariant curve

and

·         Divariant equilibria, in which both P and T are free to change independently without changing the state of the system (but bounded by the conditions defined by the univariant equilibria).

The integer in the Gibbs Phase Rule

is related to the number of intensive parameters (i.e. those that are independent of mass; such as pressure and temperature) that are being considered. Note that many phase diagrams consider only one intensive parameter (e.g. T-X_fluid, where T is intensive, and the mole fraction of fluid is related to the amount of mass of the fluid components); in this case, the Gibbs Phase Rule would be: P + F = C + 1.

It is generally the case that as the number of components increase, the variance of the system must also increase. Conversely, as the number of phases increase in the system, the variance of the system must correspondingly decrease. A corollary to Gibbs' Phase Rule is Goldschmidt's Mineralogical Phase Rule: for a given rock in equilibrium at a fixed P and T, the number of phases is less than or equal to the number of components. Geologic systems are really rather simple! This means that we have a reasonable expectation that we can successfully interpret the conditions of formation of rocks in their natural settings, and to model their behavior using the thermodynamic databases and programs presented at the end of this module.

Some Simple One-Component Examples

Let's consider the simple 1 component system for H₂O:

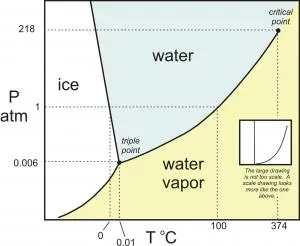
Phase diagram for the one component system H₂O. This diagram is not to scale; a scale version looks like the thumbnail in the white box.

·         The system is entirely composed of H₂O, so there is only one component present.

·         The phases present represent three states of matter: liquid (water), solid (ice), and vapor (steam). All have distinct physical properties (e.g. density, structure--or lack of, etc.) and chemical properties (e.g. ΔG_formation, molar volume etc.) so they must be considered distinct phases.

·         Note that there is only one point on this diagram where all three phases coexist in equilibrium--this "triple point" is also referred to as an invariant point; because P and T are uniquely specified, there are zero degrees of freedom.

·         Each of the curves represents a chemical reaction that describes a phase transformation: solid to liquid (melt/crystallization), liquid to vapor (boiling/condensation), solid to vapor (sublimation/deposition). There are three univariant curves around the invariant point; it is always the case that for a C-component system, there will always be C+2 univariant curves radiating around an invariant point. This relationship is further explained in the unit on the Method of Schreinemakers. There is only one degree of freedom along each of the univariant curves: you can independently change either T or P, but to maintain two coexisting phases along the curve the second variable must change by a corresponding fixed amount.

·         There are three distinct areas where only ice, liquid, or vapor exit. These are divariant fields. T and P are both free to change within these fields and you will still have only one phase (a bit hotter or colder, or compressed or expanded, but nonetheless the same phase).

·         The end of the "boiling curve", separating the liquid to vapor transition, is called the "critical point". This is a particularly interesting part of the phase diagram because beyond this region the physico-chemical properties of water and steam converge to the point where they are identical. Thus, beyond the critical point, we refer to this single phase as a "supercritical fluid".

Now, let's consider a simple 1 component system that describes the mineral phases in the aluminosilicate system:

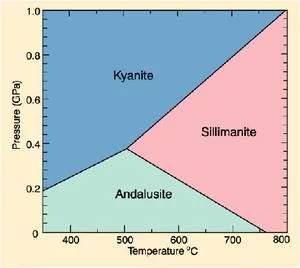
Phase diagram for the one component system Al₂SiO₅.

·         The entire system is defined by one component: Al₂SiO₅ (i.e. all the phases can be completely made of this one component)

·         There are three solid phases shown in this diagram: the polymorphs of Al₂SiO₅ andalusite, kyanite and sillimanite.

·         There is only one unique place on this diagram where all three phases can coexist in equilibrium--the invariant point at 3.8 Kb and 500^oC; at this point there are zero degrees of freedom.

·         There are three univariant reactions on this diagram, each representing the phase transitions: andalusite = sillimanite, andalusite = kyanite, and kyanite = sillimanite. In each of these reactions, either pressure or temperature can be changed independently, but for the state of the system to remain the same (i.e. two solid phases coexisting in equilibrium), the other variable must change by a fixed amount to maintain the assemblage on the univariant curve -- so there is one degree of freedom. In a later section, we will see that the univariant curves represent the condition where ΔG_rxn = 0 (i.e. the intersection of the "free energy surface" with the Pressure-Temperature plane represented by the phase diagram).

·         There are three divariant fields in which only a single mineral phase is stable. Within these fields pressure and temperature may be changed independently without changing the state of the system--thus there are two degrees of freedom in the divariant fields.

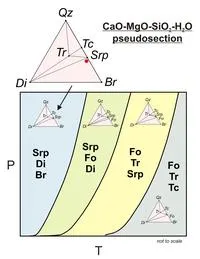
These principles extend to the more complicated binary, ternary and multi-component systems presented in the next section(s) of this module on Phase Diagrams and Pseudosections.

Assumptions

There are a number of important assumptions that must be considered when applying Gibbs' Phase Rule:

·         The relationships described by the Gibbs' Phase Rule apply the concepts of equilibrium thermodynamics. It is assumed that geologic systems have enough time to naturally equilibrate. It is also assumed that geologic systems are "closed" systems--that is the mass of the system remains essentially constant, and the system is free to consume or liberate energy to do work.

·         For geologic systems, heat and work are considered to be the major contributors to the system's energetics--that is, "P-V work" is the dominant source of energy consumed/liberated by the system. We do not consider the effects of external fields (e.g. electrical, magnetic, gravitational), and we do not consider surface energy or boundary effects.

·         No kinetic effects are considered. This may present problems with an equilibrium thermodynamics approach if metastable phases are present in the system. In natural settings it is common for a given mineral to exist under physical conditions that exceed its predicted stability limits. A good example is the persistence of kyanite into the sillimanite stability field. This particular reaction a) has a very small ΔG_rxn (and thus, a small "driving force" to make the reaction go), and b) the polymorphic reaction is of the "reconstructive" kind, and requires the breaking and reforming of strong covalent bonds. The presence of metastable phases may complicate matters in trying to determine the equilibrium conditions for stable mineral assemblages, but they are essential indicators of changing physical conditions that allow us to interpret Pressure-Temeperature-time Paths.

·         In some cases, surface reactions (e.g. sorption, catalysis) may operate in geological environment and contribute to the overall energetics of the system. Surface energies are not included in the Gibbs Phase Rule formulation.

·         Gibbs' Phase Rule cannot be applied indiscriminately. It is important to obtain the best possible characterization of the identity, composition and structural state of the phases present. For example, complex materials such as mixed layer silicates may cause problems, or minerals that exhibit a range of structural states (e.g. the alkali feldspars). An overview of analytical techniques that are used to characterize minerals, melts and fluids can be found at the companion website on Geochemical Instrumentation and Analysis

·         Recognizing these assumptions and limitations, the Gibbs Phase Rule still provides a powerful way to analyze and interpret geological systems. Although geologic systems are dynamic and often in a state of disequilibrium, the equilibrium approach demonstrates what the state of the system would be given sufficient time and energy to achieve that equilibrium. It also provides information on the phase changes or reactions that would be expected in a system that is thrown out of equilibrium due to changes in physical conditions. Thus a knowledge of the sequence of possible reactions provides important information about "pathways" in geologic systems that allow interpretations of tectonic environments, petrogenetic processes, and the evolution of geologic systems (see following chapters on Pseudosections, P-T-t Paths, and Advanced Modeling Programs (ThermoCalc, TWEEQ, PERPLEX, MELTS).

Derivation of the Phase Rule

It is important to recognize that the simple formulation of Gibbs' Phase Rule is derivative from fundamental thermodynamic principles. The Gibbs- Duhem equation establishes the relationship between the intensive parameters temperature (T) and pressure (P) and the chemical potential of all components (μ_i) in the system:
dG = Vdp - Sdt + ΣN_idμ_i
This means that there are

·         C + 2 independent variables that describe the system: P, T and one each for the chemical potential for all components, and

·         P independent equations (of the Gibbs-Duhem form) that describe the energetics of the system--one equation for each phase.

In mathematical terms, the variance (F) is determined by the difference between (C+2) variables and (P) equations. Thus,

F = C + 2 - P or as originally written, P + F = C + 2

A more extensive derivation of the phase rule can be found at the website of W. R. Salzman, Department of Chemistry, University of Arizona or this PowerPoint presentation on the derivation of the Phase Rule (PowerPoint 337kB Sep18 07) by Marty Rutstein, SUNY New Paltz.