Heat Engines
In thermodynamics, a heat engine is a system that performs the conversion of heat or thermal energy to mechanical work.
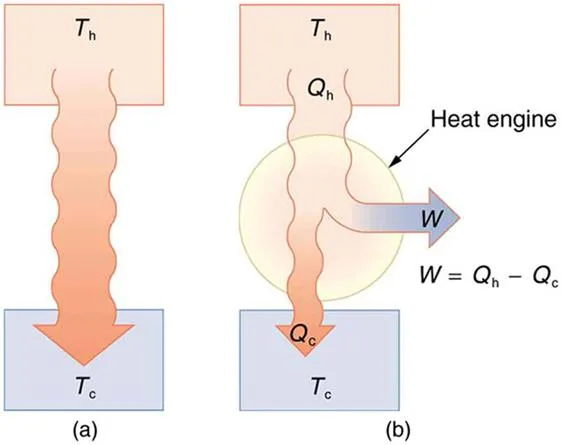
In thermodynamics, a heat engine is a system that performs the conversion of heat or thermal energy to mechanical work. Gasoline and diesel engines, jet engines, and steam turbines are all heat engines that do work by using part of the heat transfer from some source. Heat transfer from the hot object (or hot reservoir) is denoted as Qh, while heat transfer into the cold object (or cold reservoir) is Qc, and the work done by the engine is W. The temperatures of the hot and cold reservoirs are Th and Tc, respectively.

Heat Transfer: (a) Heat transfer occurs spontaneously from a hot object to a cold one, consistent with the second law of thermodynamics. (b) A heat engine, represented here by a circle, uses part of the heat transfer to do work. The hot and cold objects are called the hot and cold reservoirs. Qh is the heat transfer out of the hot reservoir, W is the work output, and Qc is the heat transfer into the cold reservoir.
Thermodynamics and Heat Engines: A brief introduction to heat engines and thermodynamic concepts such as the Carnot Engine for students.
Because the hot reservoir is heated externally, which is energy intensive, it is important that the work is done as efficiently as possible. In fact, we would like W to equal Qh, and for there to be no heat transfer to the environment (Qc=0). Unfortunately, this is impossible. The second law of thermodynamics (second expression) also states, with regard to using heat transfer to do work: It is impossible in any system for heat transfer from a reservoir to completely convert to work in a cyclical process in which the system returns to its initial state.
A cyclical process brings a system, such as the gas in a cylinder, back to its original state at the end of every cycle. Most heat engines, such as reciprocating piston engines and rotating turbines, use cyclical processes. The second law, in its second form, clearly states that such engines cannot have perfect conversion of heat transfer into work done.
Efficiency
A cyclical process brings the system back to its original condition at the end of every cycle. By definition, such a system’s internal energy U is the same at the beginning and end of every cycle—that is, ΔU=0. The first law of thermodynamics states that ΔU=Q−W, where Q is the net heat transfer during the cycle (Q=Qh−Qc) and W is the net work done by the system. Since ΔU=0 for a complete cycle, we have W=Q. Thus the net work done by the system equals the net heat transfer into the system, or
W=Qh−Qc (cyclical process),
just as shown schematically in (b).
Efficiency is one of the most important parameters for any heat engine. The problem is that in all processes, there is significant heat transfer Qc lost to the environment. In the conversion of energy to work, we are always faced with the problem of getting less out than we put in. We define the efficiency of a heat engine (Eff) to be its net work output W divided by heat transfer to the engine Qh:
