Optical reservoir computing

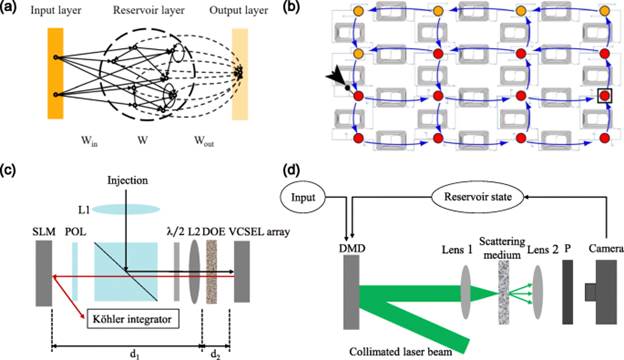
Reservoir computing (RC), which find its roots in the concept of liquid-state machine  and echo state networks , is a novel computational framework derived from recurrent neural networks (RNNs) [68]. It consists of three layers, named as input, reservoir, and output, as shown in Fig. 3(a). Different from general RNNs trained with back-propagation, such as LSTM and gated recurrent units (GRUs), only the readout coefficients denoted by Wout from the reservoir layer to the output layer need to be trained for a particular task for RC. The internal network parameters, namely the adjacency matrix Win from the input layer to the reservoir layer, and the connections inside the reservoir W are untrained, which are fixed and random or in a regular topology. In the training phase of conventional reservoir computing architectures, the reservoir state is collected at each discrete time step n following

x(n)=fNL(Win∙u(n)+W∙x(n−1))x(n)=fNL(Win∙u(n)+W∙x(n−1))

(2)

where fNL is a vector nonlinear function, u(n) is the input signal, x(n) is the reservoir state. In the case of the supervised learning, the optimal readout matrix Wout is obtained by ridge regression in general following

Wout=My∙MTx∙(Mx∙MTx+λ∙I)−1Wout=My∙MxT∙(Mx∙MxT+λ∙I)−1

where Mx is the matrix which is concatenated by the reservoir state x with some training input vectors u, My is the target matrix that is concatenated by the ground truth corresponding to the training input vectors, I is the identity matrix, and λ is the regularization coefficient which is used to avoid over-fitting. In the testing phase, the predicted output signal y(n) is calculated following

y(n)=Wout∙x(n).y(n)=Wout∙x(n).

Fig. 3

Compared with general RNNs, the training time of RC is reduced by several orders of magnitude, which speeds up the time-to-result tremendously. Besides, RC has achieved the state-of-the-art performance for many sequential tasks . Last but not least, RC is very friendly to hardware implementation . Due to the aforementioned advantages, RC has attracted more and more attentions in research community. It has be utilized in signal equalization , speech recognition , time-series prediction or classification , and de-noising in temporal sequence .

The research on RC focuses on three aspects: the expansion of the application scope of RC, the optimization of the topological structure in the reservoir, and new physical implementation. The first aspect is devoted to using RC to solve specific tasks. The second aspect is aimed to reduce the computing complexity or increase the memory capacity of RC algorithm . The third aspect is about employing novel mechanism to realize or optimize RC . Limited by the scope of this paper, we concentrate on the third aspect, especially on the optoelectronic/optical implementations of RC.

Due to its inherent parallelism and speed, photonic technology is expertly suited for hardware implementation of RC. Over the past decade, the optoelectronic/optical implementations of RC has aroused great interest of researchers . According to the way to achieve the internal connection in the reservoir, optoelectronic/optical RC can be divided into two categories: spatially distributed RC (SD-RC) and time-delayed RC (TL-RC) .

Spatially distributed RC, SD-RC

For SD-RC, it allows for the implementation of various connection topologies of the reservoir layer. In 2008, Vandoorne et al. suggested the implementation of photonic RC in an on-chip network of semiconductor optical amplifiers (SOAs) in numerical simulation, where SOAs are connected in a waterfall topology and the power-saturation behavior of SOA resembles the nonlinear function [100]. Soon after, researchers intended to optically reproduce the performance of the numerical counterparts , realizing it is energy-inefficient to driving a SOA into power saturation results. Vandoorne et al. therefore proposed and demonstrated RC on a silicon photonic chip, which consists of optical waveguides, optical splitters, and optical combiners as shown in Fig. 3(b). Reservoir nodes are indicated by the colored dots, while blue arrows indicate the topology of the network. The nonlinearity was achieved by the photo detector, for photo detector detects optical power rather than the amplitude. This approach can deal with data in the rate of 0.12 up to 12.5Gbit/s. As for the disadvantages, the number of nodes in the reservoir, namely the reservoir size is restricted by the optical losses. Besides, it is difficult to measure response on all nodes in parallel. In 2015, Brunner and Fischer demonstrated a spatially extended photonic RC which is based on the diffractive imaging of the vertical cavity surface emitting lasers (VCSEL) using a standard diffractive optical element (DOE) . The connection matrix in the reservoir is implemented by coupling between individual lasers of the VCSEL, where the bias current of each laser can be controlled separately. As shown in Fig. 3(c), an image of the VCSEL array is formed on the left side of the imaging lens. By fine-tuning the parameters of the system, after passing through the DOE beam splitter, diffractive orders of one laser will overlap with the non-diffracted image of its neighbors, thus achieving the connection of different neurons. By using the SLM located at imaging plane, the coupling weights can be controlled. The nonlinearity originates from the highly nonlinear response of the semiconductor lasers. Following the VCSEL array reservoir, a Köhler integrator and detectors are utilized to collect the integrated and weighted reservoir state. The reservoir size of this system is limited by optical aberrations of the imaging setup. Except that, miniaturization is another issue need to be addressed for commercial applications. Brunner et al. further proposed a large scale photonic recurrent neural network with 2025 diffractively coupled photonic nodes using DOE and investigated fundamental and practical limits to the size of photonic networks based on diffraction coupling . They also investigated the noise’s influence on the performance of the optoelectronic recurrent neural network . In 2018, Jonathan et al. presented a novel optical implementation of RC using light-scattering media and a DMD . As shown in Fig. 3(d), input and reservoir state are encoded on the surface of the DMD. After illuminating by the collimated laser, the encoded optical pattern pass through the multiple scattering medium, and detected by the camera. The mapping from the input to the reservoir and the internal connection in the reservoir are both realized by the optical transmission in the scattering medium instantly. Researches show the transmission matrix of the multiple scattering media is complex Gaussian matrix , thus the internal connection in the reservoir of this setup is random and fixed. The reservoir state are recorded by the camera. One prominent advantage of this approach is that the reservoir size can be scaled easily and be expanded to even millions, which is challenging for the server based on conventional von Neumann computer architectures. Nevertheless, the calculation accuracy is limited by the experimental noise and encoding strategy. They further improved the performance of this system by using phase modulation and demonstrated its feasibility for spatiotemporal chaotic systems prediction . Inspired by this research, Uttam et al. put forward an optical reservoir computer for classification of time-domain waveforms by using multimode waveguide as scattering medium .