A random sample is a sample that is chosen randomly. It could be more accurately called a randomly chosen sample. Random samples are used to avoid bias and other unwanted effects. Of course, it isn’t quite as simple as it seems: choosing a random sample isn’t as simple as just picking 100 people from 10,000 people. You have to be sure that your random sample is truly random!
Note that the word “random” in random sample doesn’t exactly fit the dictionary definition of the word. If you Google “define:random” then you’ll read that it means:
made, done, happening, or chosen without method or conscious decision.
“a random sample of 100 households”
It isn’t true that a random sample is chosen “without method of conscious decision.” Simple random sampling is one way to choose a random sample.
A simple random sample is often mentioned in elementary statistics classes, but it’s actually one of the least used techniques. In theory, it’s easy to understand. However, in practice it’s tough to perform.
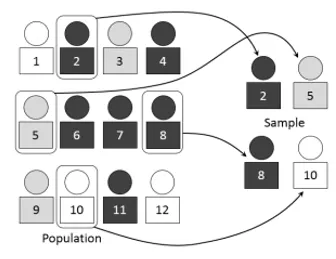
Technically, a simple random sample is a set of n objects in a population of N objects where all possible samples are equally likely to happen. Here’s a basic example of how to get a simple random sample: put 100 numbered bingo balls into a bowl (this is the population N). Select 10 balls from the bowl without looking (this is your sample n). Note that it’s important not to look as you could (unknowingly) bias the sample. While the “lottery bowl” method can work fine for smaller populations, in reality you’ll be dealing with much larger populations.

Simple random sampling of a sample “n” of 3 from a population “N” of 12. Image: Dan Kernler |Wikimedia Commons
A simple random sample is chosen in such a way that every set of individuals has an equal chance to be in the selected sample. It sounds easy, but SRS is often difficult to employ in surveys or experiments. In addition, it’s very easy for bias to creep into samples obtained with simple random sampling. Sometimes it’s impossible (either financially or time-wise) to get a realistic sampling frame (the population from which the sample is to be chosen). For example, if you wanted to study all the adults in the U.S. who had high cholesterol, the list would be practically impossible to get unless you surveyed every person in the country. Therefore other sampling methods would probably be better suited to that particular experiment.
The simplest example of SRS would be working with things like dice or cards — rolling the die or dealing cards from a deck can give you a simple random sample. But in real life you’re usually dealing with people, not cards, and that can be a challenge.
A larger population might be “All people who have had strokes in the United States.” That list of participants would be extremely hard to obtain. Where would you get such a list in the first place? You could contact individual hospitals (of which there are thousands and thousands…) and ask for a list of patients (would they even supply you with that information? If you could somehow obtain this list then you will end up with a list of 800,000 people which you then have to put into a “bowl” of some sort and choose random people for your sample. This type of situation is the type of real-life situation you’ll come across and is what makes getting a simple random sample so hard to undertake.