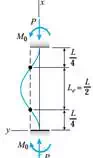
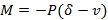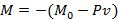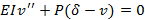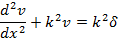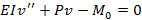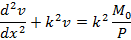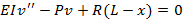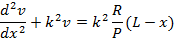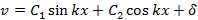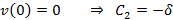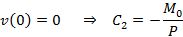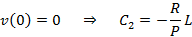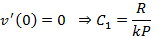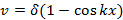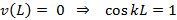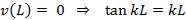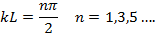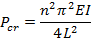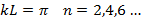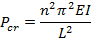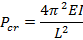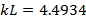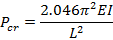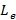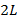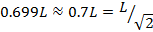Columns with other support conditions

a) The critical loads for columns with various kinds of support conditions can be determined from the differential equation of the deflection curve by following the same procedure as above

Step 1 With the column assumed to be in the buckled state, we obtain an expression for the bending moment in the column.

Step 2 Set up the differential equation of the deflection curve, using the bending-moment equation

Step 3 Solve the equation and obtain its general solution, which contains two constants of integration plus any other unknown quantities.

Step 4 Apply boundary conditions pertaining to the deflection v and the slope v^’ and obtain a set of simultaneous equations.

Step 5 Obtain the equation of deflection curve for buckled column

Step 6 Solve those equations to obtain the critical load          

	Fixed-Free column	Fixed-fixed Column	Fixed-pinned column
Step 1
Step 2
Step 3
Step 4
Step 5	Applying third boundary condition	Applying third boundary condition	Applying third boundary condition
Step 6	Lowest critical load	Lowest critical load	Lowest critical load