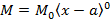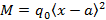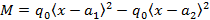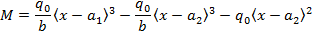Macaulay’s method

a.)Macaulay functions are used to represent quantities that “begin” at some particular point on the x-axis and have the value zero to the left of that point.

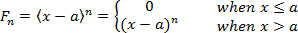
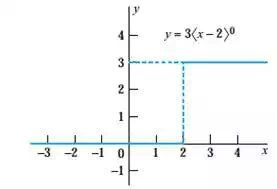
Some of the basic algebraic operations, such as addition, subtraction, and multiplication by a constant, can be performed on the Macaulay functions.

Few examples of Macaulay function

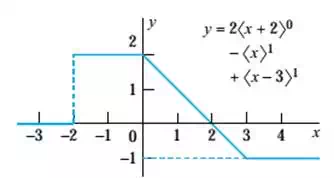
b.)How Macaulay method is used for deflection

Step 1 Find out Equivalent bending moment using Macaulay Function using following table. Last three cases (in yellow color) are rare.

Case	Load on beam	Equivalent Bending moment
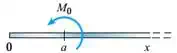
Only Moment
Only Point load
UDL till infinity
UDL only in a segment of beam
Increasing UVL till infinity
Increasing UVL only in a segment of beam
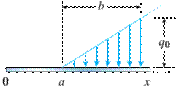
Decreasing UVL only in a segment of beam

Step 2 Choose a distance x from the left end of the beam such that there is not load/ force/ moment is acting after that. Except reaction force at right support

Step 3 Write the equivalent bending moment and substitute in the following equation

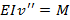
Step 4 After substitution integrate the above equation twice to obtain the equation of elastic curve with two unknown constant of integration

Step 5 Use boundary conditions to find out the value of constants

Note 1.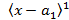 Will be integrated as a whole i.e.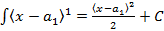 

Note 2. 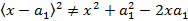. Macaulay functions do not follow the normal algebra

Step 6 Substitute the value of constants to get the equation of elastic curve. Which further cab be use to find out the value of

a. Value of deflection at any point on the beam

b. Value of slope at any point on the beam