Strain Energy

a)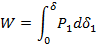

The work done by the load is equal to the area below the load-displacement curve

c) When the load stretches the bar, strains are produced. The presence of these strains increases the energy level of the bar itself. Strain energy is defined as the energy absorbed by the bar during the loading process. From the principle of conservation of energy, we know that this strain energy is equal to the work done by the load

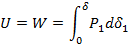
d)

i) The relationship between the load P and the elongation 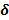 for a bar of linearly elastic material is given by the equation

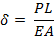
F From the first equation we see that increasing the length of a bar increases the amount of strain energy even though the load is unchanged

b)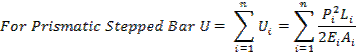

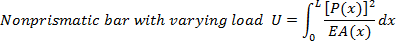
c) Strain energy is not a linear function of the loads, not even when the material is linearly elastic. Thus, it is important to realize that we cannot obtain the strain energy of a structure supporting more than one load by combining the strain energies obtained from the individual loads acting separately

d) Strain energy density: Strain energy per unit volume of material

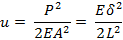
The second expression is nothing but the area under the stress-strain curve. In more general situations where the material does not follow Hooke’s law, the strain-energy density is still equal to the area below the stress-strain curve, but the area must be evaluated for each particular material.

i) Modulus of resilience: The strain-energy density of the material when it is stressed to the proportional limit. Resilience represents the ability of a material to absorb and release energy within the elastic range.

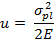
ii) Modulus of toughness: The strain-energy density when the material is stressed to the point of failure. It is equal to the area below the entire stress-strain curve. Toughness refers to the ability of a material to absorb energy without fracturing.