Bernoulli’s Principle and Equation

 

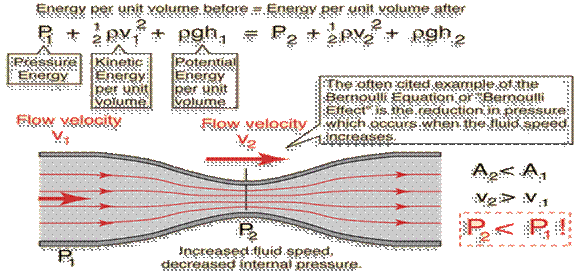
During 17^th century, Daniel Bernoulli investigated the forces present in a moving fluid, derived an equation and named it as an Bernoulli’s equation. Below image shows one of many forms of Bernoulli’s equation.
The Bernoulli equation gives an approximate equation that is valid only in inviscid regions of flow where net viscous forces are negligibly small compared to inertial, gravitational or pressure forces. Such regions occur outside of boundary layers and waves.

Despite its simplicity, Bernoulli’s Principle has proven to be a very powerful tool in fluid mechanics.
Care must be taken when applying the Bernoulli equation since it is an approximation that applies only to inviscid regions of flow. In general, frictional effects are always important very close to solid walls and directly downstream of bodies.
The motion of a particle and the path it follows are described by the velocity vector as a function of time and space coordinates and the initial position of the particle. When the flow is steady, all particles that pass through the same point follow the same path and the velocity vectors remain tangent to the path at every point.

 

Assumptions in Bernoulli’s equation:

§  Fluid is ideal and incompressible.

§  Flow is steady

§  Flow is continuous

§  Flow is non-viscous

§  Flow is irrotational

§  Applicable along a stream line.