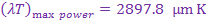BLACKBODY RADIATION
1) A body at a temperature above absolute zero emits radiation in all directions over a wide range of wavelengths. The amount of radiation energy emitted from a surface at a given wavelength depends on
a) The material of the body and
b) The condition of its surface as well as the surface temperature.
2) Therefore, different bodies may emit different amounts of radiation per unit surface area, even when they are at the same temperature. Hence we are interested in maximum amount of radiation that can be emitted by a surface at a given temperature which requires the definition of an idealized body, called a blackbody, to serve as a standard against which the radiative properties of real surfaces may be compared.
3) A blackbody is defined as a perfect emitter and absorber of radiation.
a) At a specified temperature and wavelength, no surface can emit more energy than a blackbody
b) A blackbody absorbs all incident radiation, regardless of wavelength and direction
c) A blackbody emits radiation energy uniformly in all directions per unit area normal to direction of emission
d) A blackbody is a diffuse emitter, diffuse means “independent of direction.”
4) Stefan–Boltzmann law gives the total blackbody
emissive power 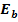 , which is the sum of the
radiation emitted over all wavelengths
, which is the sum of the
radiation emitted over all wavelengths
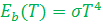
a) 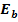 blackbody emissive
power
blackbody emissive
power
b) 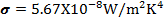 is the Stefan–Boltzmann
constant
is the Stefan–Boltzmann
constant
c) T is the absolute temperature of the surface in K
5) Spectral blackbody emissive
power 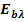 , which is the amount
of radiation energy emitted by a blackbody at an absolute temperature T per
unit time, per unit surface area, and per unit wavelength about the wavelength
, which is the amount
of radiation energy emitted by a blackbody at an absolute temperature T per
unit time, per unit surface area, and per unit wavelength about the wavelength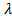 . The relation for the spectral
blackbody emissive power
. The relation for the spectral
blackbody emissive power 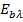 was developed by Max Planck in 1901 in conjunction with his
famous quantum theory. This relation is known as Planck’s law
was developed by Max Planck in 1901 in conjunction with his
famous quantum theory. This relation is known as Planck’s law

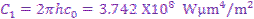
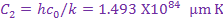
a) T is the absolute temperature of the surface in K
b)  is the wavelength of the
radiation emitted
is the wavelength of the
radiation emitted
c) 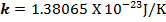 is Boltzmann’s
constant
is Boltzmann’s
constant
d) This relation is valid for a
surface in a vacuum or a gas. For other mediums, it needs to be modified
by replacing 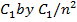 , where n is
the index of refraction of the medium.
, where n is
the index of refraction of the medium.
6)