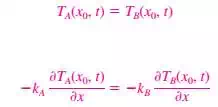BOUNDARY AND INITIAL CONDITIONS

1) The differential equations do not incorporate any information related to the conditions on the surfaces such as the surface temperature or a specified heat flux.

2) The mathematical expressions of the thermal conditions at the boundaries are called the boundary conditions.

3) From a mathematical point of view, solving a differential equation is essentially a process of removing derivatives, or an integration process, and thus the solution of a differential equation typically involves arbitrary constants. In all the above equations we have 2^nd order differential equations so we need at least 2 boundary condition to solve then completely (to get unique solution)

4) Initial Condition The temperature at any point on the body at a specified time also depends on the condition of the wall at the beginning of the heat conduction process. Such a condition, which is usually specified at time t=0, is called the initial condition, which is a mathematical expression for the temperature distribution of the medium initially

a) We need only one initial condition for a heat conduction problem regardless of the dimension since the conduction equation is first order in time.

5) Boundary Conditions There are approximately 5 kinds of boundary conditions

a) Specified Temperature Boundary Condition: For one-dimensional heat transfer through a plane wall of thickness L

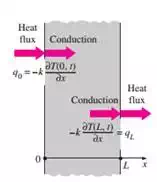
The sign of the specified heat flux is determined by inspection: positive if the heat flux is in the positive direction of the coordinate axis, and negative if it is in the opposite direction

i) Insulated Boundary

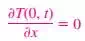
On an insulated surface, the first derivative of temperature with respect to the space variable (the temperature gradient) in the direction normal to the insulated surface is zero. This also means that the temperature function must be perpendicular to an insulated surface since the slope of temperature at the surface must be zero.

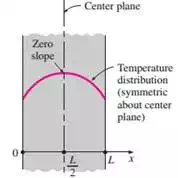
ii) Thermal Symmetry:

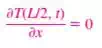
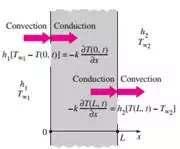
c) Convection Boundary Condition:

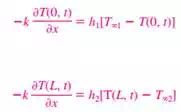
d) Radiation Boundary Condition:

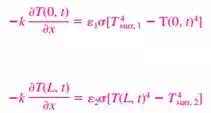
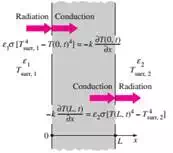
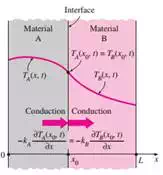
e) Interface Boundary Conditions: