Method of resolution of forces

Considering the equilibrium of the forces acting at D, we have

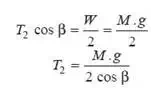
Again, considering the equilibrium of the forces acting on B. The point B is in equilibrium under the action of the following forces, as shown in Fig. 6.3 (b).

(i)               The weight of ball (w = m.g),

(ii)            The centrifugal force (FC),

(iii)          The tension in the arm (T1), and

(iv)          The tension in the link (T2).

Resolving the forces vertically,

Notes : 1. When the length of arms are equal to the length of links and the points P and D lie on the same vertical line, then

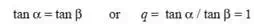
Therefore the above equation becomes

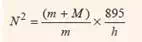
2. When the loaded sleeve moves up and down the spindle, the frictional force acts on it in a direction opposite to that of the motion of sleeve.

If F = Frictional force acting on the sleeve in newtons, then the above equations get reduced as

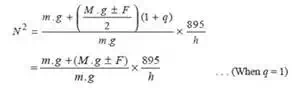
The + sign is used when the sleeve moves upwards or the governor speed increases and negative sign is used when the sleeve moves downwards or the governor speed decreases.