1) An engine, running at 150 r.p.m., drives a line shaft by means of a belt. The engine pulley is 750 mm diameter and the pulley on the line shaft being 450 mm. A 900 mm diameter pulley on the line shaft drives a 150 mm diameter pulley keyed to a dynamo shaft. Find the speed of the dynamo shaft, when 1. there is no slip, and 2. there is a slip of 2% at each drive.
Solution:
Given: N1 = 150 r.p.m. ; d1 = 750 mm ; d2 = 450 mm ; d3 = 900 mm ; d4 = 150 mm
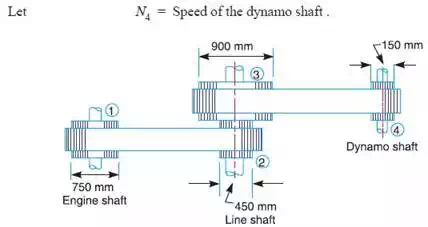
1. When there is no slip
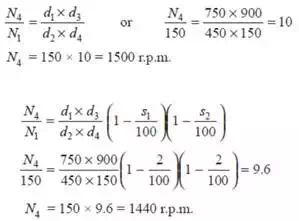
2. When there is a slip of 2% at each drive
2) Find the power transmitted by a belt running over a pulley of 600 mm diameter at 200 r.p.m. The coefficient of friction between the belt and the pulley is 0.25, angle of lap 160° and maximum tension in the belt is 2500 N.
Solution:
Given: d = 600 mm = 0.6 m ; N = 200 r.p.m. ; μ = 0.25 ; q = 160° = 160 × π/ 180 = 2.793 rad ; T1 = 2500 N We know that velocity of the belt,
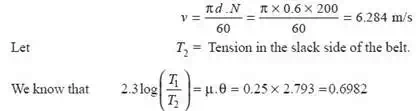
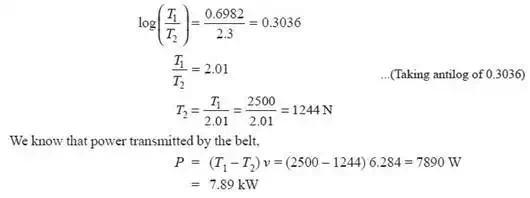
3) A casting weighing 9 kN hangs freely from a rope which makes 2.5 turns round a drum of 300 mm diameter revolving at 20 r.p.m. The other end of the rope is pulled by a man. The coefficient of friction is 0.25. Determine 1. The force required by the man, and 2. The power to raise the casting.
Solution:
Given : W = T1 = 9 kN = 9000 N ; d = 300 mm = 0.3 m ; N = 20 r.p.m. ; μ = 0.25
1. Force required by the man
Let T2 = Force required by the man.
Since the rope makes 2.5 turns round the drum, therefore angle of contact,
q= 2.5 × 2 π = 5 π rad
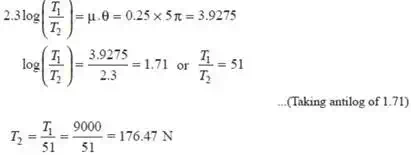
2. Power to raise the casting
We know that velocity of the rope,
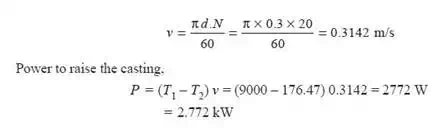
4) Two pulleys, one 450 mm diameter and the other 200 mm diameter are on parallel shafts 1.95 m apart and are connected by a crossed belt. Find the length of the belt required and the angle of contact between the belt and each pulley. What power can be transmitted by the belt when the larger pulley rotates at 200 rev/min, if the maximum permissible tension in the belt is 1 kN, and the coefficient of friction between the belt and pulley is 0.25 ?
Solution:
Given : d1 = 450 mm = 0.45 m or r1 = 0.225 m ; d2 = 200 mm = 0.2 m or r2 = 0.1 m ; x = 1.95 m ; N1 = 200 r.p.m. ; T1 = 1 kN = 1000 N ; μ = 0.25
We know that speed of the belt,
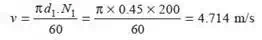
We know that length of the crossed belt,
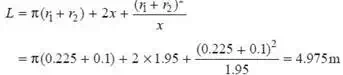
Angle of contact between the belt and each pulley

Power transmitted
Let T2 = Tension in the slack side of the belt.
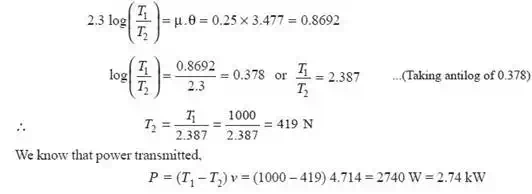 We know that
We know that
5) A shaft rotating at 200 r.p.m. drives another shaft at 300 r.p.m. and transmits 6 kW through a belt. The belt is 100 mm wide and 10 mm thick. The distance between the shafts is 4m. The smaller pulley is 0.5 m in diameter. Calculate the stress in the belt, if it is 1. an open belt drive, and 2. a cross belt drive. Take μ =0.3.
Solution:
Given : N1 = 200 r.p.m. ; N2 = 300 r.p.m. ; P = 6 kW = 6 × 103 W ; b = 100 mm ; t = 10 mm ; x = 4 m ; d2 =
0.5 m ; μ = 0.3
Let s = Stress in the belt.
1. Stress in the belt for an open belt drive
First of all, let us find out the diameter of larger pulley (d1). We know that
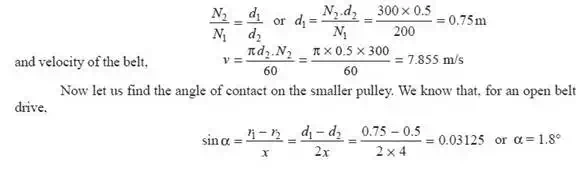
By solving the above two equations
T1= 1267 N and T2= 503 N
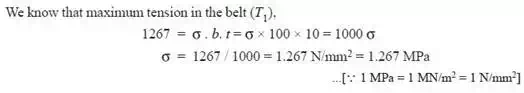
Stress in the belt for a cross belt drive
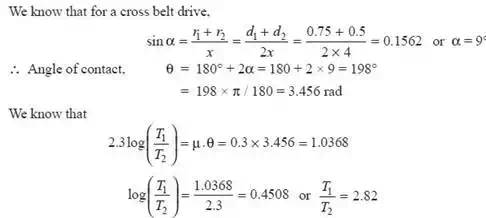
By solving the above equations
T1 = 1184 N and T2 = 420 N
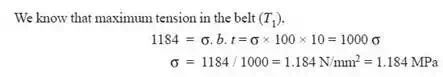
6) Determine the width of a 9.75 mm thick leather belt required to transmit 15 kW from a motor running at 900 r.p.m. The diameter of the driving pulley of the motor is 300 mm. The driven pulley runs at 300 r.p.m. and the distance between the centre of two pulleys is 3 metres. The density of the leather is 1000 kg/m3. The maximum allowable stress in the leather is 2.5 MPa. The coefficient of friction between the leather and pulley is 0.3. Assume open belt drive and neglect the sag and slip of the belt.
Solution:
Given: t = 9.75 mm = 9.75 × 10–3 m ; P = 15 kW = 15 × 10 3 W ; N1 = 900 r.p.m. ; d1 = 300 mm = 0.3 m ; N2 = 300 r.p.m. ; x = 3m ; r = 1000 kg/m3 ; s = 2.5 MPa = 2.5 × 106 N/m2 ; μ = 0.3
First of all, let us find out the diameter of the driven pulley (d2). We know that
On solving above two equations we get T1= 1806 N


