Motion of a link

Consider two points A and B on a rigid link AB, as shown in Fig.  (a). Let one of the extremities

(B) of the link move relative to A, in a clockwise direction. Since the distance from A to B remains the same, therefore there can be no relative motion between A and B, along the line AB. It is thus obvious, that the relative motion of B with respect to A must be perpendicular to AB.

Hence velocity of any point on a link with respect to another point on the same link is always perpendicular to the line joining these points on the configuration (or space) diagram.

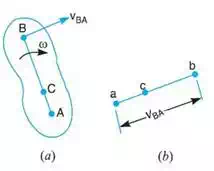
The relative velocity of B with respect to A (i.e. vBA) is represented by the vector ab and is perpendicular to the line AB as shown in Fig. (b).

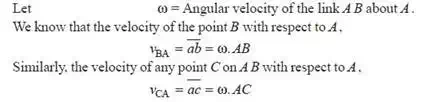
From the above two equations

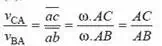
Thus, we see from above equation that the point c on the vector ab divides it in the same ratio as C divides the link AB.