Kinematics
of Machines in Mechanical Engineering
|
When
we refer to the study of the kinematics of machines, we’re referring to the
relationship between machine parts and how those parts behave as they move
through their ranges of motion. What this means is that there is
particular concern with the relative motion of machine parts, that is, how
they relate to each other, their position, distance, velocity, and
acceleration. When
speaking of the kinematics of machines, a mechanism is considered to be like
a chain with a system of links that are connected together. This
chain is constrained, meaning that independent movement of one part is not
possible. These parts are interconnected, and they all move
relative to each other. Motion in any one link of this kinematic
chain will result in a relative and predictable motion to each of the
others. Now, by “chain,” I don’t necessarily mean a chain in the
physical sense, but rather the fact that the parts of the mechanism are
linked together. To
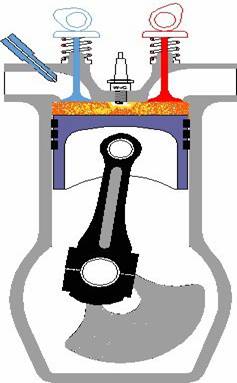
illustrate what I’m talking about, let’s consider the gasoline engine shown
in Figure 1 below.
Figure
1 To
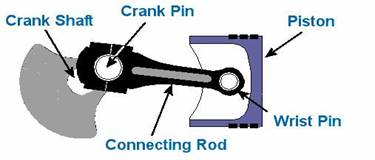
help you follow along, let’s turn the engine on its side and name the parts
of one of its kinematic chains. This is shown in Figure 2.
Figure
2
Suppose
you want to analyze how fast the engine’s
piston is moving at any given instant during its
operation. Suppose further that you know how fast the crank shaft
is turning. Where would your analysis begin? Well,
while studying the motions of machine parts, it’s helpful to draw the parts
first in skeletal form so that only those dimensions that affect their
motions are considered. Let’s represent the kinematic chain of
Figure 2 in skeletal form. See Figure 3
Figure
3
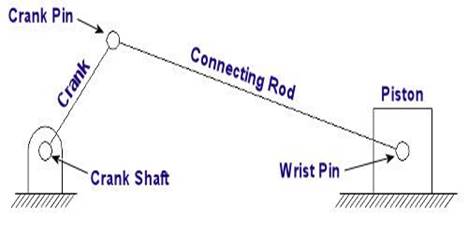
Lastly,
we embellish the skeleton with the depiction of angles that are at play as
the parts of our engine move, and we add the relevant symbols that will allow
us to build the equations we’ll be working with. This is shown in
Figure 4.
Figure
4
So,
as the engine runs, the crank AB rotates around the center of
the crank shaft A. The connecting rod BC is attached to the piston
at the wrist pin C. The piston moves back and forth as AB
rotates. Now here is where things get a little hairy, and for some
of you it may look somewhat like code or a foreign language. The
tangential velocity VB of the crank pin B is shown in Figure
4 as a vector. A vector is something which depicts both a
magnitude and direction. And since VB is a
“tangential velocity,” it is moving in a direction which is at a right angle,
that is, at a 90-degree angle in relation to the crank AB. This
relationship will always exist between VB and the crank AB. In
the posed scenario, VB is a velocity, so let’s say its
magnitude will be in units of inches per second. The magnitude of
the vector VB is then directly related to the speed of
crankshaft AB and is determined by this equation: VB =
2∏RN ÷ 60 Referring
to Figure 4, R is the distance between the center of
the crank shaft and the center of the
crank pin in inches. N is the rotational speed of crank AB in revolutions per
minute (rpm). If
one knows the crank angle X, the crank length R, and the connecting rod
length L in Figure 4, they can then use trigonometry to determine the
velocity of the piston. This velocity is represented by the vector
VC, and its magnitude, or value, would be found by using the
following equation… VC =
[VB] × [sin(X + Y)] ÷ [sin(90° – Y)] …where
the angle Y is found by: Y =
[sin-1(R ÷ L)] × [sin(X)] Analysis
of kinematics of machines would become even more complicated when complex
mechanisms like oddly shaped linkages, cams and followers, and gear trains
are involved. |