Friction Results in Heat and Lost Work Within a Compound Pulley

Last time we saw how the presence of friction reduces mechanical advantage in an engineering scenario utilizing a compound pulley.   We also learned that the actual amount of effort, or force, required to lift an object is a combination of the portion of the force which is hampered by friction and an idealized scenario which is friction-free.   here we’ll begin our exploration into how friction results in reduced work input, manifested as heat energy lost to the environment.   The net result is that work input does not equal work output and some of Mr. Toga’s labour is unproductive.

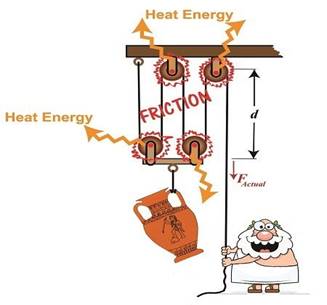
Friction Results in Heat and Lost Work Within a Compound Pulley

In a past topic, we showed how the actual force required to lift our urn is a combination of F, an ideal friction-free work effort by Mr. Toga, and F_F , the extra force he must exert to overcome friction present in the wheels,

F_Actual = F + F_F                        (1)

            Mr. Toga is clearly working to lift his turn, and generally speaking his work effort, WI, is defined as the force he employs multiplied by the length, d, of rope that he pulls out of the compound pulley during lifting.   Mathematically that is,

WI = F_Actual × d                      (2)

            To see what happens when friction enters the picture, we’ll first substitute equation (1) into equation (2) to get WI in terms of F and F_F,

WI = (F + F_F ) × d                   (3)

Multiplying through by d, equation (3) becomes,

WI  =  (F × d )+ (F_F  × d)          (4)

            In equation (4) WI is divided into two terms.   Next time we’ll see how one of these terms is beneficial to our lifting scenario, while the other is not.